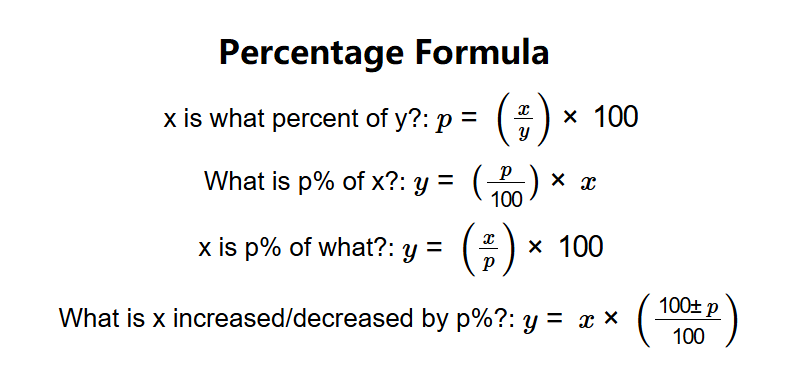1. What is the Percentage Calculator?
Definition: This calculator performs various percentage calculations, including finding what percentage one number is of another, calculating a percentage of a number, determining the whole given a part and percentage, or calculating a value after a percentage increase or decrease.
Purpose: It assists users in solving percentage-related problems in finance, education, statistics, and everyday scenarios like calculating discounts, tips, or growth rates.
2. How Does the Calculator Work?
The calculator supports four modes with the following equations:
- x is what percent of y?: \( p = \left(\frac{x}{y}\right) \times 100 \)
- What is p% of x?: \( y = \left(\frac{p}{100}\right) \times x \)
- x is p% of what?: \( y = \left(\frac{x}{p}\right) \times 100 \)
- What is x increased/decreased by p%?: \( y = x \times \left(\frac{100 \pm p}{100}\right) \)
Where:
- \( x \): First input value (part, whole, or initial value depending on mode);
- \( y \): Second input value (whole, percentage, or percentage change depending on mode);
- \( p \): Percentage (%).
Steps:
- Select the calculation mode from the dropdown.
- Enter the two input values (labels adjust based on the mode).
- For increase/decrease mode, specify whether to increase or decrease.
- The calculator validates inputs (e.g., no division by zero, non-negative values where applicable).
- Calculate the result using the appropriate formula.
- Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Percentage Calculations
Percentage calculations are essential for:
- Financial Planning: Calculating discounts, taxes, or interest rates.
- Educational Use: Determining test scores or grades as percentages.
- Business Applications: Analyzing profit margins, growth rates, or sales increases.
- Everyday Scenarios: Figuring out tips, sales discounts, or budget proportions.
4. Using the Calculator
Example 1 (x is what percent of y?): What percentage is 45 of 50?
- x: \( x = 45 \);
- y: \( y = 50 \);
- Percentage: \( p = \left(\frac{45}{50}\right) \times 100 = 90 \);
- Result: \( p = 90.0000\% \).
Example 2 (What is p% of x?): What is 20% of 150?
- x: \( x = 150 \);
- p: \( p = 20 \);
- y: \( y = \left(\frac{20}{100}\right) \times 150 = 30 \);
- Result: \( y = 30.0000 \).
Example 3 (x is p% of what?): 30 is 15% of what?
- x: \( x = 30 \);
- p: \( p = 15 \);
- y: \( y = \left(\frac{30}{15}\right) \times 100 = 200 \);
- Result: \( y = 200.0000 \).
Example 4 (What is x increased by p%?): What is 100 increased by 10%?
- x: \( x = 100 \);
- p: \( p = 10 \);
- Change Type: Increase;
- y: \( y = 100 \times \left(\frac{100 + 10}{100}\right) = 110 \);
- Result: \( y = 110.0000 \).
5. Frequently Asked Questions (FAQ)
Q: What happens if I enter a zero for the denominator in certain modes?
A: The calculator will display an error message since division by zero is undefined (e.g., in "x is what percent of y?" or "x is p% of what?").
Q: Can I use negative numbers?
A: For most modes, inputs must be non-negative to reflect typical percentage use cases. However, in the increase/decrease mode, the result can be negative if the decrease exceeds 100%.
Q: How precise is the result?
A: The result is displayed with 4 decimal places, or in scientific notation if the value is less than 0.001, ensuring high precision.
 Home
Home
 Back
Back