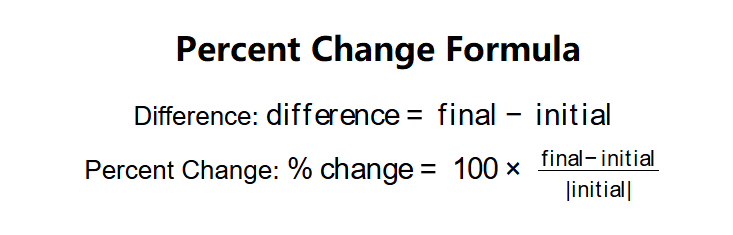Percent Change Calculator

1. What is the Percent Change Calculator?

Definition: This calculator determines the percentage change and numerical difference between an initial value and a final value. The percent change is calculated using the formula $ \% \text{ change} = 100 \times \frac{\text{final} - \text{initial}}{|\text{initial}|} $, and the difference is $ \text{difference} = \text{final} - \text{initial} $.

Purpose: It helps users quantify both the relative change (as a percentage) and the absolute change (numerical difference) between two values, useful in finance, science, and everyday scenarios.

2. How Does the Calculator Work?

The calculator uses the following equations:

Difference: $ \text{difference} = \text{final} - \text{initial} $
Percent Change: $ \% \text{ change} = 100 \times \frac{\text{final} - \text{initial}}{|\text{initial}|} $

Where:

$ \text{initial} $: The starting value;
$ \text{final} $: The ending value;
$ |\text{initial}| $: The absolute value of the initial value (to handle negative initial values).

Steps:

Enter the initial value.
Enter the final value.
The calculator checks that the initial value is not zero to avoid division by zero in the percent change calculation.
Calculate the difference by subtracting the initial value from the final value.
Calculate the percent change by dividing the difference by the absolute value of the initial value and multiplying by 100.
Display both results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Percent Change and Difference Calculation

Calculating percent change and difference is crucial for:

Financial Analysis: Measuring stock price changes, profit growth, or expense reductions, and understanding the absolute change in value.
Scientific Studies: Analyzing growth rates and absolute changes in populations, chemical concentrations, or experimental results.
Business Decisions: Evaluating sales performance or price changes, both relatively and absolutely.
Educational Use: Teaching concepts of relative and absolute change in mathematics.

4. Using the Calculator

Example 1 (Price Increase): Calculate the percent change and difference in price from $50 to $75:

Initial: $ \text{initial} = 50 $;
Final: $ \text{final} = 75 $;
Difference: $ \text{difference} = 75 - 50 = 25 $;
Percent Change: $ 100 \times \frac{75 - 50}{|50|} = 100 \times \frac{25}{50} = 50 $;
Result: $ \text{difference} = 25.0000 $, $ \% \text{ change} = 50.0000\% $.

Example 2 (Negative Initial Value): Calculate the percent change and difference from -3.5 to 1.5:

Initial: $ \text{initial} = -3.5 $;
Final: $ \text{final} = 1.5 $;
Difference: $ \text{difference} = 1.5 - (-3.5) = 5 $;
Percent Change: $ 100 \times \frac{1.5 - (-3.5)}{|-3.5|} = 100 \times \frac{5}{3.5} \approx 142.8571 $;
Result: $ \text{difference} = 5.0000 $, $ \% \text{ change} = 142.8571\% $.

5. Frequently Asked Questions (FAQ)

Q: Why is the absolute value used in the denominator for percent change?
A: The absolute value ensures the percent change calculation is meaningful even if the initial value is negative, as it measures the magnitude of the change relative to the initial value's size.

Q: What does a negative difference or percent change mean?
A: A negative difference or percent change indicates a decrease from the initial value to the final value (e.g., a price drop).

Q: How precise are the results?
A: Both the difference and percent change are displayed with 4 decimal places, or in scientific notation if the value is less than 0.001, ensuring high precision.