1. What is the Pentagon Calculator?
Definition: This calculator computes the geometrical properties of a regular pentagon, a 5-sided polygon where all sides and angles are equal.
Purpose: It assists in geometry, design, and architecture by providing key measurements of a regular pentagon, useful in fields like tiling, construction, and pattern design.
2. How Does the Calculator Work?
The calculator uses the following formulas:
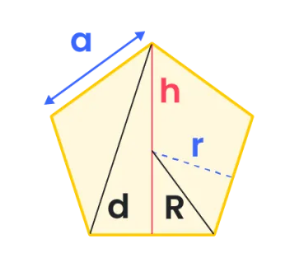
- Perimeter: \( P = 5a \)
- Area: \( A = \frac{a^2 \times \sqrt{25 + 10\sqrt{5}}}{4} \)
- Diagonal: \( d = a \times \frac{1 + \sqrt{5}}{2} \)
- Height: \( h = a \times \sqrt{\frac{5 + 2\sqrt{5}}{2}} \)
- Incircle Radius/Apothem: \( r = \frac{a}{2} \times \sqrt{\frac{5 + 2\sqrt{5}}{5}} \)
Steps:
- Enter the side length \( a \) of the pentagon along with its unit (mm, cm, m, in, ft, or yd).
- Convert the side length to meters for calculation.
- Compute the pentagon properties in meters (for lengths) and square meters (for area).
- Convert each result to its selected output unit independently.
- Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Pentagon Calculations
Calculating pentagon properties is essential for:
Design: Creating efficient tiling patterns in architecture and flooring, such as pentagonal tiles.
Construction: Designing structures like the Pentagon building with precise measurements.
Education: Exploring geometric properties and symmetry in mathematics.
4. Using the Calculator
Example 1: Calculate the pentagon properties:
- Side Length: \( a = 5 \, \text{in} \);
- Output Units: Area in in², Lengths in in;
- Convert to meters: \( a = 5 \times 0.0254 = 0.127 \, \text{m} \);
- Side in m: \( a = 0.127 \, \text{m} \);
- Diagonal in m: \( d = a \times \frac{1 + \sqrt{5}}{2} = 0.127 \times \frac{1 + \sqrt{5}}{2} \approx 0.2055 \, \text{m} \);
- Height in m: \( h = a \times \sqrt{\frac{5 + 2\sqrt{5}}{2}} = 0.127 \times \sqrt{\frac{5 + 2\sqrt{5}}{2}} \approx 0.2191 \, \text{m} \);
- Perimeter in m: \( P = 5a = 5 \times 0.127 = 0.635 \, \text{m} \);
- Area in m²: \( A = \frac{a^2 \times \sqrt{25 + 10\sqrt{5}}}{4} = \frac{(0.127)^2 \times \sqrt{25 + 10\sqrt{5}}}{4} \approx 0.02782 \, \text{m}^2 \);
- Circumcircle Radius in m: \( R = \frac{a}{2} \times \sqrt{\frac{5 + \sqrt{5}}{2}} = \frac{0.127}{2} \times \sqrt{\frac{5 + \sqrt{5}}{2}} \approx 0.1049 \, \text{m} \);
- Incircle Radius in m: \( r = \frac{a}{2} \times \sqrt{\frac{5 + 2\sqrt{5}}{5}} = \frac{0.127}{2} \times \sqrt{\frac{5 + 2\sqrt{5}}{5}} \approx 0.0875 \, \text{m} \);
- Convert to in and in²: \( a = 0.127 \div 0.0254 = 5 \, \text{in} \), \( d = 0.2055 \div 0.0254 \approx 8.0906 \, \text{in} \), \( h = 0.2191 \div 0.0254 \approx 8.6260 \, \text{in} \), \( P = 0.635 \div 0.0254 = 25 \, \text{in} \), \( A = 0.02782 \div 0.00064516 \approx 43.1045 \, \text{in}^2 \), \( R = 0.1049 \div 0.0254 \approx 4.1299 \, \text{in} \), \( r = 0.0875 \div 0.0254 \approx 3.4449 \, \text{in} \);
- Results: \( a = 5.0000 \, \text{in} \), \( d = 8.0906 \, \text{in} \), \( h = 8.6260 \, \text{in} \), \( P = 25.0000 \, \text{in} \), \( A = 43.1045 \, \text{in}^2 \), \( R = 4.1299 \, \text{in} \), \( r = 3.4449 \, \text{in} \).
Example 2: Calculate the pentagon properties:
- Side Length: \( a = 2 \, \text{in} \);
- Output Units: Side in in, Diagonal in cm, Height in in, Perimeter in cm, Area in in², Circumcircle Radius in yd, Incircle Radius in mm;
- Convert to meters: \( a = 2 \times 0.0254 = 0.0508 \, \text{m} \);
- Side in m: \( a = 0.0508 \, \text{m} \);
- Diagonal in m: \( d = a \times \frac{1 + \sqrt{5}}{2} = 0.0508 \times \frac{1 + \sqrt{5}}{2} \approx 0.0822 \, \text{m} \);
- Height in m: \( h = a \times \sqrt{\frac{5 + 2\sqrt{5}}{2}} = 0.0508 \times \sqrt{\frac{5 + 2\sqrt{5}}{2}} \approx 0.0876 \, \text{m} \);
- Perimeter in m: \( P = 5a = 5 \times 0.0508 = 0.254 \, \text{m} \);
- Area in m²: \( A = \frac{a^2 \times \sqrt{25 + 10\sqrt{5}}}{4} = \frac{(0.0508)^2 \times \sqrt{25 + 10\sqrt{5}}}{4} \approx 0.00445 \, \text{m}^2 \);
- Circumcircle Radius in m: \( R = \frac{a}{2} \times \sqrt{\frac{5 + \sqrt{5}}{2}} = \frac{0.0508}{2} \times \sqrt{\frac{5 + \sqrt{5}}{2}} \approx 0.0420 \, \text{m} \);
- Incircle Radius in m: \( r = \frac{a}{2} \times \sqrt{\frac{5 + 2\sqrt{5}}{5}} = \frac{0.0508}{2} \times \sqrt{\frac{5 + 2\sqrt{5}}{5}} \approx 0.0350 \, \text{m} \);
- Convert results: \( a = 0.0508 \div 0.0254 = 2 \, \text{in} \), \( d = 0.0822 \times 100 = 8.22 \, \text{cm} \), \( h = 0.0876 \div 0.0254 \approx 3.4488 \, \text{in} \), \( P = 0.254 \times 100 = 25.4 \, \text{cm} \), \( A = 0.00445 \div 0.00064516 \approx 6.8975 \, \text{in}^2 \), \( R = 0.0420 \div 0.9144 \approx 0.0459 \, \text{yd} \), \( r = 0.0350 \times 1000 \approx 35.00 \, \text{mm} \);
- Results: \( a = 2.0000 \, \text{in} \), \( d = 8.2200 \, \text{cm} \), \( h = 3.4488 \, \text{in} \), \( P = 25.4000 \, \text{cm} \), \( A = 6.8975 \, \text{in}^2 \), \( R = 0.0459 \, \text{yd} \), \( r = 35.0000 \, \text{mm} \).
5. Frequently Asked Questions (FAQ)
Q: What is a regular pentagon?
A: A regular pentagon is a 5-sided polygon where all sides and angles are equal, with each interior angle measuring 108°.
Q: How many diagonals does a regular pentagon have?
A: A regular pentagon has 5 diagonals, all equal in length, forming a pentagram.
Q: Can I use this calculator for irregular pentagons?
A: No, this calculator is designed for regular pentagons only. Irregular pentagons require different methods to compute their properties.
 Home
Home
 Back
Back