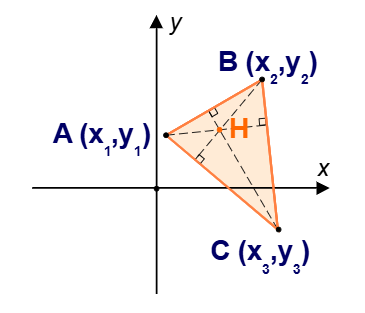
1. What is the Orthocenter Calculator?
Definition: This calculator computes the orthocenter of a triangle, which is the point where the three altitudes of the triangle intersect. An altitude is a perpendicular line from a vertex to the line containing the opposite side.
Purpose: It assists in geometry and engineering by providing the orthocenter coordinates, useful in triangle analysis, design, and educational purposes.
2. How Does the Calculator Work?
The calculator follows these steps:
- Slope of \( AB \): \( \text{slope}_{AB} = \frac{y_2 - y_1}{x_2 - x_1} \)
- Perpendicular slope to \( AB \): \( \text{perp slope}_{AB} = -\frac{1}{\text{slope}_{AB}} \)
- Line perpendicular to \( AB \) through \( C \): \( y = \text{perp slope}_{AB} \times x + (y_3 - \text{perp slope}_{AB} \times x_3) \)
- Slope of \( BC \): \( \text{slope}_{BC} = \frac{y_3 - y_2}{x_3 - x_2} \)
- Perpendicular slope to \( BC \): \( \text{perp slope}_{BC} = -\frac{1}{\text{slope}_{BC}} \)
- Line perpendicular to \( BC \) through \( A \): \( y = \text{perp slope}_{BC} \times x + (y_1 - \text{perp slope}_{BC} \times x_1) \)
- Solve for orthocenter by finding the intersection of the two lines.
Steps:
- Enter the coordinates of the three vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \) along with their units (mm, cm, m, in, ft, or yd).
- Convert all coordinates to meters for calculation.
- Compute the orthocenter coordinates in meters.
- Convert the orthocenter coordinates to the selected output units independently.
- Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Orthocenter Calculations
Calculating the orthocenter is essential for:
Geometry: Understanding triangle properties and relationships between altitudes.
Engineering: Analyzing structures and forces in triangular frameworks.
Education: Teaching concepts of triangle geometry and coordinate systems.
4. Using the Calculator
Example 1: Calculate the orthocenter (replicating the Omni Calculator example):
- Vertex A: \( (1, 1) \, \text{(unitless)} \);
- Vertex B: \( (3, 5) \, \text{(unitless)} \);
- Vertex C: \( (7, 2) \, \text{(unitless)} \);
- Output Units: unitless (select meters for consistency);
- Coordinates in meters: \( A(1, 1) \), \( B(3, 5) \), \( C(7, 2) \);
- Slope of \( AB \): \( \frac{5 - 1}{3 - 1} = 2 \);
- Perpendicular slope to \( AB \): \( -\frac{1}{2} \);
- Line through \( C(7, 2) \): \( y - 2 = -\frac{1}{2} (x - 7) \implies y = -\frac{1}{2}x + \frac{11}{2} \);
- Slope of \( BC \): \( \frac{2 - 5}{7 - 3} = -\frac{3}{4} \);
- Perpendicular slope to \( BC \): \( \frac{4}{3} \);
- Line through \( A(1, 1) \): \( y - 1 = \frac{4}{3} (x - 1) \implies y = \frac{4}{3}x - \frac{1}{3} \);
- Solve: \( -\frac{1}{2}x + \frac{11}{2} = \frac{4}{3}x - \frac{1}{3} \implies \frac{35}{6} = \frac{11}{6}x \implies x = \frac{35}{11} \approx 3.1818 \);
- \( y = \frac{4}{3} \times \frac{35}{11} - \frac{1}{3} = \frac{43}{11} \approx 3.9091 \);
- Results: \( h_x = 3.1818 \), \( h_y = 3.9091 \).
Example 2: Calculate the orthocenter:
- Vertex A: \( (0, 0) \, \text{in} \);
- Vertex B: \( (4, 0) \, \text{in} \);
- Vertex C: \( (0, 3) \, \text{in} \);
- Output Units: \( h_x \) in in, \( h_y \) in cm;
- Convert to meters: \( A(0, 0) \), \( B(4 \times 0.0254, 0) = (0.1016, 0) \), \( C(0, 3 \times 0.0254) = (0, 0.0762) \);
- Slope of \( AB \): \( \frac{0 - 0}{0.1016 - 0} = 0 \);
- Perpendicular slope to \( AB \): undefined (vertical line);
- Line through \( C(0, 0.0762) \): \( x = 0 \);
- Slope of \( BC \): \( \frac{0.0762 - 0}{0 - 0.1016} = -0.75 \);
- Perpendicular slope to \( BC \): \( \frac{4}{3} \);
- Line through \( A(0, 0) \): \( y = \frac{4}{3}x \);
- Intersection at \( x = 0 \), \( y = 0 \);
- Convert results: \( h_x = 0 \, \text{in} \), \( h_y = 0 \times 100 = 0 \, \text{cm} \);
- Results: \( h_x = 0.0000 \, \text{in} \), \( h_y = 0.0000 \, \text{cm} \).
5. Frequently Asked Questions (FAQ)
Q: What is the orthocenter of a triangle?
A: The orthocenter is the point where the three altitudes of a triangle intersect. An altitude is a line from a vertex perpendicular to the opposite side (or its extension).
Q: Can the orthocenter be outside the triangle?
A: Yes, in obtuse triangles, the orthocenter lies outside the triangle. In right triangles, it coincides with the right-angle vertex, and in acute triangles, it is inside.
Q: What if the points are collinear?
A: If the three points are collinear, the triangle is degenerate, and no orthocenter exists. The calculator will display an error in such cases.
 Home
Home
 Back
Back