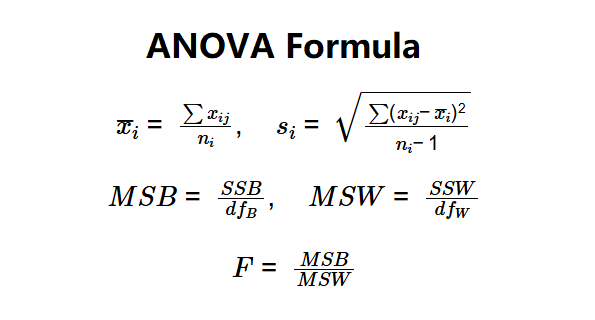One-Way ANOVA Calculator

ANOVA Calculator: One-Way Analysis of Variance Calculator

Group	Values (comma, space, or line break separated)	Action
Group 1
Group 2

1. What is a One-Way ANOVA Calculator?

Definition: This One-way ANOVA Test Calculator helps you to quickly and easily produce a one-way analysis of variance (ANOVA) table that includes all relevant information from the observation data set including sums of squares, mean squares, degrees of freedom, F-values.

Purpose: Helps researchers and statisticians assess whether observed differences in group means are due to real effects or random chance, commonly used in fields like psychology, biology, and education.

2. How Does the Calculator Work?

The calculator follows these steps:

Step 1: Collect Group Data

\( x_{ij} \text{ for groups } i = 1, 2, \ldots, k \)

Where:

\( x_{ij} \): Value \( j \) in group \( i \)
\( k \): Number of groups

Step 2: Calculate Group Statistics

\( \bar{x}_i = \frac{\sum x_{ij}}{n_i}, \quad s_i = \sqrt{\frac{\sum (x_{ij} - \bar{x}_i)^2}{n_i - 1}} \)

Where:

\( \bar{x}_i \): Mean of group \( i \)
\( s_i \): Standard deviation of group \( i \)
\( n_i \): Number of observations in group \( i \)

Step 3: Compute Sums of Squares

\( SSB = \sum n_i (\bar{x}_i - \bar{x})^2, \quad SSW = \sum \sum (x_{ij} - \bar{x}_i)^2, \quad SST = SSB + SSW \)

Where:

\( SSB \): Sum of Squares Between Groups
\( SSW \): Sum of Squares Within Groups
\( SST \): Total Sum of Squares
\( \bar{x} \): Overall mean

Step 4: Degrees of Freedom

\( df_B = k - 1, \quad df_W = N - k, \quad df_T = N - 1 \)

Where:

\( df_B \): Degrees of Freedom Between
\( df_W \): Degrees of Freedom Within
\( df_T \): Total Degrees of Freedom
\( N \): Total number of observations

Step 5: Mean Squares

\( MSB = \frac{SSB}{df_B}, \quad MSW = \frac{SSW}{df_W} \)

Step 6: F-Statistic

\( F = \frac{MSB}{MSW} \)

Step 7: P-Value

The p-value is calculated using the F-distribution with \( df_B \) and \( df_W \). A low p-value (e.g., < 0.05) indicates significant differences between group means.

Steps:

Enter values for each group, separated by commas, spaces, or line breaks.
Add or delete groups as needed (minimum two).
Calculate group statistics and ANOVA table components.
Display results with 4 decimal places for precision.

3. Importance of One-Way ANOVA

One-Way ANOVA is crucial for:

Comparing Groups: Determines if differences in means are statistically significant across multiple groups.
Research Applications: Used in experiments to test treatments, teaching methods, or product variations.
Decision Making: Informs whether observed differences warrant further investigation or action.

4. Using the Calculator

Example 1: Groups: [5, 7, 9], [6, 8, 10], [4, 6, 8]

Group Means: 7, 8, 6
Overall Mean: \( \frac{(5+7+9+6+8+10+4+6+8)}{9} = 7 \)
SSB: \( 3 \times (7-7)^2 + 3 \times (8-7)^2 + 3 \times (6-7)^2 = 6 \)
SSW: \( (5-7)^2 + (7-7)^2 + (9-7)^2 + (6-8)^2 + (8-8)^2 + (10-8)^2 + (4-6)^2 + (6-6)^2 + (8-6)^2 = 16 \)
SST: \( 6 + 16 = 22 \)
df: \( df_B = 3-1 = 2 \), \( df_W = 9-3 = 6 \), \( df_T = 9-1 = 8 \)
MSB: \( \frac{6}{2} = 3 \), MSW: \( \frac{16}{6} \approx 2.6667 \)
F: \( \frac{3}{2.6667} \approx 1.125 \)
Result: ANOVA table with SSB = 6.0000, SSW = 16.0000, F ≈ 1.1250, etc.

Example 2: Groups: [10, 12, 14], [8, 9, 10], [11, 13, 15]

Similar calculations yield different SSB, SSW, and F values, indicating potential significant differences.

5. Frequently Asked Questions (FAQ)

Q: What if I have fewer than two groups?
A: The calculator requires at least two groups with valid data, or an error will be displayed. Delete buttons are disabled when only two groups remain.

Q: What does a significant F-statistic mean?
A: It suggests at least one group mean differs significantly from the others, warranting post-hoc tests like Tukey’s HSD.

Q: What if assumptions (normality, equal variances) are violated?
A: Consider non-parametric alternatives like the Kruskal-Wallis test if assumptions are not met.