Nth Root Calculator

1. What is the Nth Root Calculator?

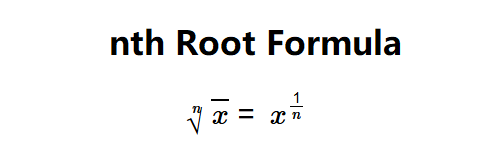
Definition: This calculator computes the \( n \)-th root of a number, which is a value that, when multiplied by itself \( n \) times, equals the original number.

Purpose: It helps students, educators, and professionals find the principal (real) \( n \)-th root of any number, useful in mathematics, physics, and geometry.

2. How Does the Calculator Work?

The calculator computes the \( n \)-th root using the following mathematical principle:

\[ \sqrt[n]{x} = y \quad \text{such that} \quad y^n = x \]

It can also be expressed as an exponent:

\[ \sqrt[n]{x} = x^{\frac{1}{n}} \]

Steps:

Enter a number (\( x \)), which can be positive or negative.
Enter the degree of the root (\( n \)), which determines the type of root (e.g., 3 for cube root, 4 for fourth root).
Click "Calculate" to compute the \( n \)-th root.
The result is the principal (real) \( n \)-th root, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Nth Root Calculation

Calculating the \( n \)-th root is crucial for:

Geometry: Determines the edge length of geometric shapes given their volume (e.g., a cube with volume 27 cm³ has an edge length of 3 cm using the cube root).
Mathematics: Solves equations involving higher-order terms and is used in number theory.
Physics: Applies in problems involving scaling laws or relationships with higher powers.
Education: Helps students understand inverse operations to exponentiation and explore properties of numbers.

4. Using the Calculator

Example 1 (Cube Root): Find the cube root of 27:

Input: \( x = 27 \), \( n = 3 \);
Cube Root: \( \sqrt[3]{27} = 3 \), since \( 3 \times 3 \times 3 = 27 \);
Result: \( 3.0000 \).

Example 2 (Fourth Root of a Negative Number): Find the fourth root of -16:

Input: \( x = -16 \), \( n = 4 \);
Error: The fourth root of a negative number is not a real number, as even roots of negative numbers result in complex numbers.

5. Frequently Asked Questions (FAQ)

Q: Can the \( n \)-th root be calculated for negative numbers?
A: Yes, if \( n \) is odd, the \( n \)-th root of a negative number is negative. For example, \( \sqrt[3]{-8} = -2 \). However, if \( n \) is even, the result is not real (e.g., \( \sqrt[4]{-16} \) is complex).

Q: What happens if the degree is negative?
A: A negative degree computes the reciprocal of the \( n \)-th root. For example, \( x^{-1/3} = \frac{1}{\sqrt[3]{x}} \). However, this calculator does not support negative degrees for zero inputs.

Q: What is a perfect \( n \)-th power?
A: A perfect \( n \)-th power is a number whose \( n \)-th root is an integer. For example, 16 is a perfect fourth power because \( \sqrt[4]{16} = 2 \), and 2 is an integer.