Multiplicative Inverse Calculator

Number Type:

Numerator:

Denominator:

Number:

Whole Number:

Numerator:

Denominator:

1. What is the Multiplicative Inverse Calculator?

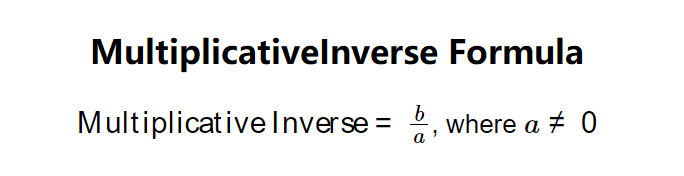
Definition: This calculator computes the multiplicative inverse (or reciprocal) of a number. The multiplicative inverse of a number \( \frac{a}{b} \) is \( \frac{b}{a} \), such that their product equals 1.

Purpose: It helps users quickly find the multiplicative inverse of any non-zero number, including integers, decimals, fractions, and mixed numbers, which is useful in mathematics, algebra, and related fields.

2. How Does the Calculator Work?

The multiplicative inverse of a number \( \frac{a}{b} \) is computed as:

\( \text{Multiplicative Inverse} = \frac{b}{a} \), where \( a \neq 0 \)

Steps:

Select the type of number: a simple fraction, an integer/decimal, or a mixed number.
Enter the number using the appropriate fields (numerator and denominator for fractions, whole number part and fraction for mixed numbers).
Click "Calculate" to compute the multiplicative inverse.
The result is displayed, formatted in scientific notation if less than 0.001 or greater than 100,000, otherwise with 4 decimal places.

3. Importance of the Multiplicative Inverse

The multiplicative inverse is important for:

Algebra: Solving equations by dividing numbers (e.g., \( x \cdot \frac{1}{x} = 1 \)).
Physics: Calculating resistances in electrical circuits.
Finance: Computing interest rates and exchange rates.
Everyday Applications: Determining unit prices, like price per ounce.

4. Using the Calculator

Example 1 (Decimal): Find the multiplicative inverse of 3.25:

Input: Number Type: An integer/decimal, Number: 3.25;
Result: \( \frac{1}{3.25} = \frac{4}{13} \approx 0.3077 \).

Example 2 (Mixed Number): Find the multiplicative inverse of \( 1\frac{3}{8} \):

Input: Number Type: A mixed number, Whole: 1, Numerator: 3, Denominator: 8;
Result: \( \frac{8}{11} \approx 0.7273 \).

5. Frequently Asked Questions (FAQ)

Q: Why can't the input number be zero?
A: The multiplicative inverse of zero is undefined because \( 0 \times \text{any number} = 0 \), which cannot equal 1.

Q: How does the calculator handle fractions?
A: For a fraction \( \frac{a}{b} \), the calculator computes the inverse as \( \frac{b}{a} \), swapping the numerator and denominator.

Q: Why does the result appear in scientific notation?
A: If the result is less than 0.001 or greater than 100,000, it is displayed in scientific notation for readability; otherwise, it shows 4 decimal places.