1. What is the Moment of Inertia Calculator?
Definition: This calculator computes the moment of inertia (also known as the mass moment of inertia or the area moment of inertia) of various shapes about their centroidal axes (x and y). The moment of inertia quantifies an object's resistance to rotational acceleration.
Purpose: It assists in engineering and physics by providing essential values for structural analysis, dynamics, and design, particularly in beam bending and rotational motion studies.
2. How Does the Calculator Work?
The calculator uses the following formulas for each shape:
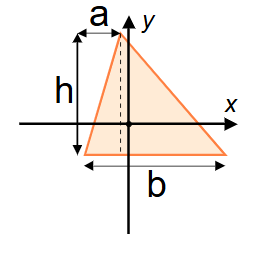
- Triangle: \( I_x = \frac{\text{width} \times \text{height}^3}{36} \)
- \( I_y = \frac{(\text{height} \times \text{width}^3 - \text{height} \times \alpha \times \text{width}^2 + \text{width} \times \text{height} \times \alpha^2)}{36} \)
Steps:
- Select the shape from the dropdown menu.
- Enter the required dimensions for the selected shape along with their units (mm, cm, m, in, ft, or yd).
- Convert all inputs to meters for calculation.
- Compute the moments of inertia in meters⁴ based on the shape-specific formulas.
- Convert the results to the selected output units (mm⁴, cm⁴, m⁴, in⁴, ft⁴, or yd⁴).
- Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Moment of Inertia Calculations
Calculating the moment of inertia is essential for:
Structural Engineering: Analyzing beam deflection and stress distribution.
Mechanical Engineering: Designing rotating machinery like flywheels and turbines.
Physics: Understanding rotational dynamics and angular momentum.
Education: Teaching concepts of mass distribution and rotational motion.
4. Using the Calculator
Example 1 (Rectangle): Calculate the moment of inertia:
- Width: \( 4 \, \text{in} \);
- Height: \( 6 \, \text{in} \);
- Output Units: in⁴;
- Convert to meters: \( \text{width} = 4 \times 0.0254 = 0.1016 \, \text{m} \), \( \text{height} = 6 \times 0.0254 = 0.1524 \, \text{m} \);
- Ix in m⁴: \( I_x = \frac{\text{width} \times \text{height}^3}{12} = \frac{0.1016 \times (0.1524)^3}{12} \approx 0.00002992 \, \text{m}^4 \);
- Iy in m⁴: \( I_y = \frac{\text{height} \times \text{width}^3}{12} = \frac{0.1524 \times (0.1016)^3}{12} \approx 0.00001333 \, \text{m}^4 \);
- Convert to in⁴:
\( I_x = 0.00002992 \div 4.162314256e-7 \approx 71.8796 \, \text{in}^4 \), \( I_y = 0.00001333 \div 4.162314256e-7 \approx 32.0249 \, \text{in}^4 \);
- Result: \( I_x = 71.8796 \, \text{in}^4 \), \( I_y = 32.0249 \, \text{in}^4 \).
Example 2 (Circle): Calculate the moment of inertia:
- Radius: \( 3 \, \text{in} \);
- Output Units: Ix in cm⁴, Iy in in⁴;
- Convert to meters: \( \text{radius} = 3 \times 0.0254 = 0.0762 \, \text{m} \);
- Ix = Iy in m⁴: \( I_x = I_y = \frac{\pi}{4} \times \text{radius}^4 = \frac{\pi}{4} \times (0.0762)^4 \approx 0.00002646 \, \text{m}^4 \);
- Convert results: \( I_x = 0.00002646 \times 10^8 = 2646 \, \text{cm}^4 \), \( I_y = 0.00002646 \div 4.162314256e-7 \approx 63.5727 \, \text{in}^4 \);
- Result: \( I_x = 2646.0000 \, \text{cm}^4 \), \( I_y = 63.5727 \, \text{in}^4 \).
5. Frequently Asked Questions (FAQ)
Q: What is the moment of inertia?
A: The moment of inertia measures an object's resistance to rotational acceleration, depending on the distribution of its mass or area relative to the axis of rotation.
Q: Why are the axes centroidal?
A: The formulas calculate the moment of inertia about the centroidal axes (passing through the geometric center), which is standard for structural analysis as it simplifies calculations.
Q: Can I calculate the moment of inertia for other shapes?
A: This calculator supports common shapes (Triangle, Rectangle, Circle, Semicircle, Ellipse, Regular Hexagon). Other shapes require different formulas or methods, such as the parallel axis theorem for non-centroidal axes.
 Home
Home
 Back
Back