Magic Square Calculator

1. What is the Magic Square Calculator?

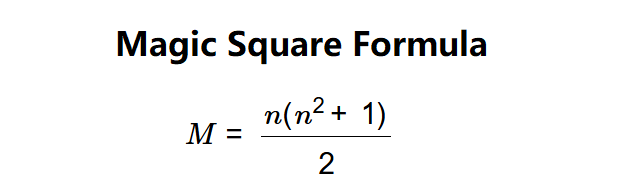
Definition: This calculator generates a magic square of size \( n \times n \), filled with distinct positive integers from 1 to \( n^2 \), such that the sum of each row, column, and main diagonal equals the magic constant \( M = \frac{n(n^2 + 1)}{2} \).

Purpose: It helps users explore the properties of magic squares, which are mathematical puzzles with applications in combinatorics, number theory, and recreational mathematics.

2. How Does the Calculator Work?

The calculator uses different methods depending on the order of the magic square:

For \( n = 1 \): A trivial 1x1 square with the number 1.
For odd \( n \) (3, 5, 7, 9): Uses the Siamese method (de la Loubère's method).
For doubly even \( n \) (4, 8): Fills numbers sequentially and swaps along main and anti-diagonals.
For singly even \( n \) (6, 10): Divides the square into four smaller odd-order squares, adjusts values, and swaps specific columns.

The magic constant is calculated as:

\[ M = \frac{n(n^2 + 1)}{2} \]

Steps:

Enter the size \( n \) of the magic square (numbers between 1 and 10).
Click "Calculate" to generate the magic square.
The result is displayed as a grid.

3. Importance of Magic Squares

Magic squares are important for:

Recreational Mathematics: They are engaging puzzles that challenge logical and mathematical thinking.
Combinatorics: They are used to study permutations and arrangements, with applications in probability and statistics.
Historical Significance: Magic squares have been studied for centuries, appearing in ancient cultures like China and Europe, often with mystical significance.
Educational Value: They help students develop problem-solving skills and understand mathematical patterns.

4. Using the Calculator

Example 1 (4x4 Magic Square): Generate a 4x4 magic square:

Input: \( n = 4 \);
Magic Constant: \( M = \frac{4(4^2 + 1)}{2} = \frac{4 \times 17}{2} = 34 \);
Result: A 4x4 grid where each row, column, and diagonal sums to 34.

Example 2 (6x6 Magic Square): Generate a 6x6 magic square:

Input: \( n = 6 \);
Magic Constant: \( M = \frac{6(6^2 + 1)}{2} = \frac{6 \times 37}{2} = 111 \);
Result: A 6x6 grid where each row, column, and diagonal sums to 111.

5. Frequently Asked Questions (FAQ)

Q: Why is a 2x2 magic square impossible?
A: A 2x2 magic square with distinct integers 1 to 4 cannot exist because the sum of numbers 1 to 4 is 10, requiring each row, column, and diagonal to sum to 5, which is mathematically impossible with distinct integers.

Q: What is the magic constant?
A: The magic constant \( M \) is the sum that each row, column, and diagonal must equal in a magic square. For an \( n \times n \) magic square with numbers 1 to \( n^2 \), it is given by \( M = \frac{n(n^2 + 1)}{2} \).

Q: Can I generate magic squares larger than 10x10?
A: This calculator limits the size to 10x10 to ensure computational feasibility and readability. Larger squares can be generated with more advanced methods or tools.