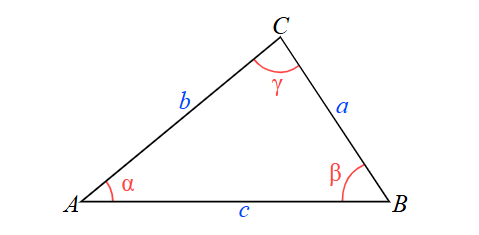
1. What is the Law of Cosines Calculator?
Definition: This calculator applies the Law of Cosines to solve triangles in two modes: SAS (side-angle-side) to find the third side given two sides and the included angle, and SSS (side-side-side) to find all three angles given the three sides. The Law of Cosines relates the sides and angles of a triangle as follows: \( c^2 = a^2 + b^2 - 2ab \cos(C) \), where \( a \), \( b \), and \( c \) are the sides, and \( C \) is the angle opposite side \( c \).
Purpose: It is used to solve triangles when the Law of Sines is insufficient, with applications in geometry, physics, engineering, and navigation.
2. How Does the Calculator Work?
The calculator uses the Law of Cosines in two modes:
- SAS Mode (Find Side): \( c^2 = a^2 + b^2 - 2ab \cos(C) \), where \( a \) and \( b \) are the given sides, and \( C \) is the included angle.
- SSS Mode (Find Angles):
- \( \cos(A) = \frac{b^2 + c^2 - a^2}{2bc} \), so \( A = \arccos\left(\frac{b^2 + c^2 - a^2}{2bc}\right) \)
- \( \cos(B) = \frac{a^2 + c^2 - b^2}{2ac} \), so \( B = \arccos\left(\frac{a^2 + c^2 - b^2}{2ac}\right) \)
- \( \cos(C) = \frac{a^2 + b^2 - c^2}{2ab} \), so \( C = \arccos\left(\frac{a^2 + b^2 - c^2}{2ab}\right) \)
Where:
- \( a, b, c \): Sides of the triangle
- \( A, B, C \): Angles opposite sides \( a \), \( b \), and \( c \), respectively
Unit Conversions:
- Input Sides:
- Millimeters (mm): \( \text{m} = \text{mm} / 1000 \)
- Centimeters (cm): \( \text{m} = \text{cm} / 100 \)
- Meters (m): No conversion needed
- Inches (in): \( \text{m} = \text{in} \times 0.0254 \)
- Feet (feet): \( \text{m} = \text{feet} \times 0.3048 \)
- Yards (yard): \( \text{m} = \text{yard} \times 0.9144 \)
- Input Angle (SAS Mode):
- Degrees (deg): Directly input in degrees
- Radians (rad): Directly input in radians
- Gradians (gon): \( \text{rad} = \text{gon} \times \frac{\pi}{200} \)
- Turns (tr): \( \text{rad} = \text{tr} \times 2\pi \)
- Minutes of Arc (arcmin): \( \text{rad} = \text{deg2rad}(\text{arcmin} / 60) \)
- Seconds of Arc (arcsec): \( \text{rad} = \text{deg2rad}(\text{arcsec} / 3600) \)
- Milliradians (mrad): \( \text{rad} = \text{mrad} / 1000 \)
- Microradians (urad): \( \text{rad} = \text{urad} / 1000000 \)
- π Radians (x π rad): \( \text{rad} = \text{x π rad} \times \pi \)
- Output Angle (SSS Mode):
- Degrees (deg): \( \text{deg} = \text{rad} \times \frac{180}{\pi} \)
- Radians (rad): Default output
- Gradians (gon): \( \text{gon} = \text{rad} \times \frac{200}{\pi} \)
- Turns (tr): \( \text{tr} = \text{rad} \times \frac{1}{2\pi} \)
- Minutes of Arc (arcmin): \( \text{arcmin} = \text{deg} \times 60 \)
- Seconds of Arc (arcsec): \( \text{arcsec} = \text{deg} \times 3600 \)
- Milliradians (mrad): \( \text{mrad} = \text{rad} \times 1000 \)
- Microradians (urad): \( \text{urad} = \text{rad} \times 1000000 \)
- π Radians (x π rad): \( \text{x π rad} = \text{rad} \times \frac{1}{\pi} \)
Steps:
- Select the calculation mode (SAS or SSS).
- For SAS: Enter two sides \( a \) and \( b \), their units, the included angle \( C \), and its unit.
- For SSS: Enter the three sides \( a \), \( b \), and \( c \), and their units.
- Click "Calculate" to compute the unknown side (SAS) or angles (SSS).
- Adjust the output unit for the result(s) using the dropdown(s).
- The results are displayed with 4 decimal places in the chosen units.
3. Importance of the Law of Cosines
The Law of Cosines is crucial for:
- Geometry: Solving triangles when the Law of Sines is insufficient (e.g., in SAS or SSS cases).
- Physics: Calculating resultant forces or displacements involving non-right angles.
- Engineering: Designing structures, analyzing trusses, and navigation.
- Astronomy: Determining distances and angles between celestial bodies.
4. Using the Calculator
Example 1 (SAS Mode):
Find side \( c \) in a triangle with sides \( a = 3 \, \text{cm} \), \( b = 4 \, \text{cm} \), and included angle \( C = 60^\circ \).
- Select the mode "SAS (2 sides + angle between)".
- Enter \( a = 3 \), \( b = 4 \), selecting "cm" for both, and \( C = 60 \), with angle unit as "deg".
- Choose "cm" as the output unit for side \( c \).
- Click "Calculate" to compute:
- \( c^2 = a^2 + b^2 - 2ab \cos(C) = 3^2 + 4^2 - 2 \times 3 \times 4 \times \cos(60^\circ) = 9 + 16 - 24 \times 0.5 = 25 - 12 = 13 \)
- \( c = \sqrt{13} \approx 3.6056 \, \text{cm} \)
Example 2 (SSS Mode):
Find angles \( A \), \( B \), and \( C \) in a triangle with sides \( a = 3 \, \text{cm} \), \( b = 4 \, \text{cm} \), and \( c = 3 \, \text{cm} \), with output in degrees.
- Select the mode "SSS (three sides)".
- Enter \( a = 3 \), \( b = 4 \), and \( c = 3 \), selecting "cm" for each side.
- Choose "deg" as the output unit for all angles.
- Click "Calculate" to compute:
- \( \cos(A) = \frac{b^2 + c^2 - a^2}{2bc} = \frac{4^2 + 3^2 - 3^2}{2 \times 4 \times 3} = \frac{16 + 9 - 9}{24} = \frac{16}{24} = \frac{2}{3} \approx 0.6667 \)
- \( A = \arccos\left(\frac{2}{3}\right) \approx 48.1897^\circ \)
- \( \cos(B) = \frac{a^2 + c^2 - b^2}{2ac} = \frac{3^2 + 3^2 - 4^2}{2 \times 3 \times 3} = \frac{9 + 9 - 16}{18} = \frac{2}{18} = \frac{1}{9} \approx 0.1111 \)
- \( B = \arccos\left(\frac{1}{9}\right) \approx 83.6206^\circ \)
- \( \cos(C) = \frac{a^2 + b^2 - c^2}{2ab} = \frac{3^2 + 4^2 - 3^2}{2 \times 3 \times 4} = \frac{9 + 16 - 9}{24} = \frac{16}{24} = \frac{2}{3} \approx 0.6667 \)
- \( C = \arccos\left(\frac{2}{3}\right) \approx 48.1897^\circ \)
5. Frequently Asked Questions (FAQ)
Q: What is the Law of Cosines?
A: The Law of Cosines is a formula that relates the sides and angles of a triangle: \( c^2 = a^2 + b^2 - 2ab \cos(C) \), where \( a \), \( b \), and \( c \) are the sides, and \( C \) is the angle opposite side \( c \). It generalizes the Pythagorean theorem for non-right triangles.
Q: When should I use the Law of Cosines?
A: Use the Law of Cosines in SAS mode when you know two sides and the included angle to find the third side, or in SSS mode when you know all three sides to find the angles. It’s particularly useful when the Law of Sines cannot be applied directly.
Q: What are the different angle units?
A: Angles can be measured in various units:
- Degrees (deg): 360° in a full circle.
- Radians (rad): \( 2\pi \) in a full circle.
- Gradians (gon): 400 gon in a full circle.
- Turns (tr): 1 turn is a full circle.
- Minutes of Arc (arcmin): 60 arcmin per degree.
- Seconds of Arc (arcsec): 3600 arcsec per degree.
- Milliradians (mrad): 1000 mrad per radian.
- Microradians (urad): 1000000 urad per radian.
- π Radians (x π rad): Expressed as a multiple of π.
Law of Cosines Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back