1. What is the Hexagon Calculator?
Definition: This calculator computes the geometrical properties of a regular hexagon, a 6-sided polygon where all sides and angles are equal.
Purpose: It assists in geometry, design, and architecture by providing key measurements of a regular hexagon, useful in fields like tiling, engineering, and natural pattern analysis.
2. How Does the Calculator Work?
The calculator uses the following formulas:
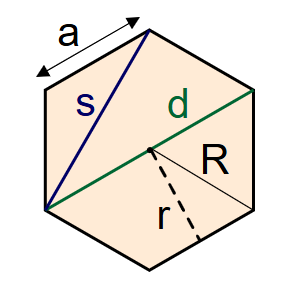
- Area: \( A = \frac{3 \sqrt{3}}{2} a^2 \)
- Perimeter: \( P = 6a \)
- Long Diagonal: \( d = 2a \)
- Short Diagonal: \( s = \sqrt{3} a \)
- Circumradius: \( R = a \)
- Apothem/Inradius: \( r = \frac{\sqrt{3}}{2} a \)
Steps:
- Enter the side length \( a \) of the hexagon along with its unit (mm, cm, m, in, ft, or yd).
- Convert the side length to meters for calculation.
- Compute the hexagon properties in meters (for lengths) and square meters (for area).
- Convert each result to its selected output unit independently.
- Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Hexagon Calculations
Calculating hexagon properties is essential for:
Nature: Understanding patterns like honeycombs, where hexagons minimize material use while maximizing space.
Design: Creating efficient tiling patterns in architecture and flooring.
Engineering: Designing structures with optimal strength-to-weight ratios.
Education: Exploring geometric properties and symmetry in mathematics.
4. Using the Calculator
Example 1: Calculate the hexagon properties:
- Side Length: \( a = 5 \, \text{in} \);
- Output Units: Area in in², Lengths in in;
- Convert to meters: \( a = 5 \times 0.0254 = 0.127 \, \text{m} \);
- Area in m²: \( A = \frac{3 \sqrt{3}}{2} a^2 = \frac{3 \sqrt{3}}{2} \times (0.127)^2 \approx 0.04193 \, \text{m}^2 \);
- Perimeter in m: \( P = 6a = 6 \times 0.127 = 0.762 \, \text{m} \);
- Long Diagonal in m: \( d = 2a = 2 \times 0.127 = 0.254 \, \text{m} \);
- Short Diagonal in m: \( s = \sqrt{3} a = \sqrt{3} \times 0.127 \approx 0.21997 \, \text{m} \);
- Circumradius in m: \( R = a = 0.127 \, \text{m} \);
- Apothem in m: \( r = \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{2} \times 0.127 \approx 0.10999 \, \text{m} \);
- Convert to in and in²: \( A = 0.04193 \div 0.00064516 \approx 64.9519 \, \text{in}^2 \), \( P = 0.762 \div 0.0254 = 30 \, \text{in} \), \( d = 0.254 \div 0.0254 = 10 \, \text{in} \), \( s = 0.21997 \div 0.0254 \approx 8.6602 \, \text{in} \), \( R = 0.127 \div 0.0254 = 5 \, \text{in} \), \( r = 0.10999 \div 0.0254 \approx 4.3301 \, \text{in} \);
- Results: \( A = 64.9519 \, \text{in}^2 \), \( P = 30.0000 \, \text{in} \), \( d = 10.0000 \, \text{in} \), \( s = 8.6602 \, \text{in} \), \( R = 5.0000 \, \text{in} \), \( r = 4.3301 \, \text{in} \).
Example 2: Calculate the hexagon properties:
- Side Length: \( a = 2 \, \text{in} \);
- Output Units: Area in in², Perimeter in cm, Long Diagonal in ft, Short Diagonal in in, Circumradius in yd, Apothem in mm;
- Convert to meters: \( a = 2 \times 0.0254 = 0.0508 \, \text{m} \);
- Area in m²: \( A = \frac{3 \sqrt{3}}{2} a^2 = \frac{3 \sqrt{3}}{2} \times (0.0508)^2 \approx 0.006709 \, \text{m}^2 \);
- Perimeter in m: \( P = 6a = 6 \times 0.0508 = 0.3048 \, \text{m} \);
- Long Diagonal in m: \( d = 2a = 2 \times 0.0508 = 0.1016 \, \text{m} \);
- Short Diagonal in m: \( s = \sqrt{3} a = \sqrt{3} \times 0.0508 \approx 0.08799 \, \text{m} \);
- Circumradius in m: \( R = a = 0.0508 \, \text{m} \);
- Apothem in m: \( r = \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{2} \times 0.0508 \approx 0.04399 \, \text{m} \);
- Convert results: \( A = 0.006709 \div 0.00064516 \approx 10.3923 \, \text{in}^2 \), \( P = 0.3048 \times 100 = 30.48 \, \text{cm} \), \( d = 0.1016 \div 0.3048 \approx 0.3333 \, \text{ft} \), \( s = 0.08799 \div 0.0254 \approx 3.4642 \, \text{in} \), \( R = 0.0508 \div 0.9144 \approx 0.0556 \, \text{yd} \), \( r = 0.04399 \times 1000 \approx 43.99 \, \text{mm} \);
- Results: \( A = 10.3923 \, \text{in}^2 \), \( P = 30.4800 \, \text{cm} \), \( d = 0.3333 \, \text{ft} \), \( s = 3.4642 \, \text{in} \), \( R = 0.0556 \, \text{yd} \), \( r = 43.9900 \, \text{mm} \).
5. Frequently Asked Questions (FAQ)
Q: What is a regular hexagon?
A: A regular hexagon is a 6-sided polygon where all sides and angles are equal, with each interior angle measuring 120°.
Q: Why are hexagons common in nature?
A: Hexagons are efficient for tiling and packing, minimizing material use while maximizing space, as seen in honeycombs and other natural structures.
Q: Can I use this calculator for irregular hexagons?
A: No, this calculator is designed for regular hexagons only. Irregular hexagons require different methods to compute their properties.
 Home
Home
 Back
Back