Harmonic Mean Calculator

1. What is the Harmonic Mean Calculator?

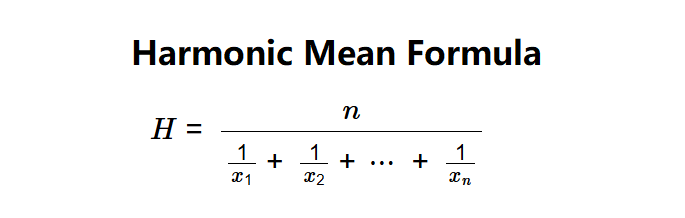
Definition: This calculator computes the harmonic mean of a set of positive numbers, which is defined as the reciprocal of the arithmetic mean of the reciprocals of the numbers. For \( n \) numbers \( x_1, x_2, \ldots, x_n \), the harmonic mean \( H \) is given by \( H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}} \).

Purpose: It helps users calculate the harmonic mean, which is useful in scenarios involving rates, ratios, and averages, such as speed, resistance, and financial analysis.

2. How Does the Calculator Work?

The harmonic mean \( H \) of \( n \) positive numbers is calculated using the formula:

\[ H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}} \]

This can be rewritten as:

\[ H = \left( \frac{\sum_{i=1}^n \frac{1}{x_i}}{n} \right)^{-1} \]

Steps:

Enter at least two positive numbers (can be decimals).
Add or remove numbers as needed using the "Add Number" and "Remove Number" buttons.
Click "Calculate" to compute the harmonic mean.
The result is displayed, formatted in scientific notation if less than 0.001 or greater than 100,000, otherwise with 4 decimal places.
An explanation of the calculation process is provided.

3. Importance of the Harmonic Mean

The harmonic mean is important for:

Rates and Ratios: It is the appropriate average for rates, such as speeds or resistances (e.g., calculating the average speed for a round trip).
Finance: It is used in financial calculations, such as averaging price-to-earnings ratios, where reciprocals are meaningful.
Statistics: It provides a measure of central tendency that emphasizes smaller values more than the arithmetic mean, useful in skewed distributions.
Practical Applications: It applies to scenarios like calculating the effective resistance of parallel resistors or the average rate of work.

4. Using the Calculator

Example 1 (Average Speed): Calculate the harmonic mean of speeds 60 km/h and 80 km/h for a round trip:

Input: Number 1: 60, Number 2: 80;
Sum of reciprocals: \( \frac{1}{60} + \frac{1}{80} = 0.0167 + 0.0125 = 0.0292 \);
Harmonic mean: \( H = \frac{2}{0.0292} \approx 68.57 \);
Result: 68.5700.

Example 2 (Three Numbers): Calculate the harmonic mean of 2, 4, and 8:

Input: Number 1: 2, Number 2: 4, Number 3: 8;
Sum of reciprocals: \( \frac{1}{2} + \frac{1}{4} + \frac{1}{8} = 0.5 + 0.25 + 0.125 = 0.875 \);
Harmonic mean: \( H = \frac{3}{0.875} \approx 3.4286 \);
Result: 3.4286.

5. Frequently Asked Questions (FAQ)

Q: Why must the numbers be positive?
A: The harmonic mean involves the reciprocals of the numbers, and the reciprocal of zero or a negative number is undefined or negative, which would not produce a meaningful harmonic mean.

Q: How does the harmonic mean differ from the arithmetic mean?
A: The harmonic mean gives more weight to smaller values, making it suitable for rates and ratios, while the arithmetic mean treats all values equally. For example, the arithmetic mean of 60 and 80 is 70, but their harmonic mean is approximately 68.57.

Q: Why does the result appear in scientific notation?
A: If the result is less than 0.001 or greater than 100,000, it is displayed in scientific notation for readability; otherwise, it shows 4 decimal places.