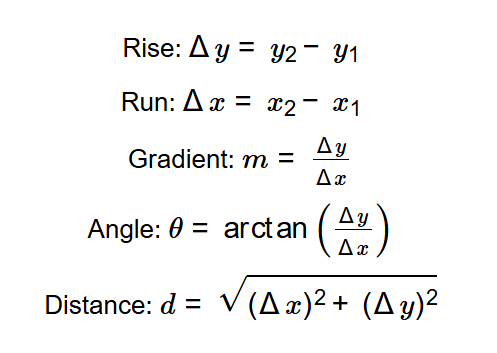1. What is the Gradient Calculator?
Definition: This calculator computes the rise, run, gradient, angle, and distance between two points in 2D space.
Purpose: It assists students, engineers, and architects in analyzing slopes, angles, and distances for applications in geometry, construction, and physics.
2. How Does the Calculator Work?
The calculator computes:
- Rise: \( \Delta y = y_2 - y_1 \)
- Run: \( \Delta x = x_2 - x_1 \)
- Gradient: \( m = \frac{\Delta y}{\Delta x} \)
- Angle: \( \theta = \arctan\left(\frac{\Delta y}{\Delta x}\right) \)
- Distance: \( d = \sqrt{(\Delta x)^2 + (\Delta y)^2} \)
Where:
- \( (x_1, y_1) \): Coordinates of the first point
- \( (x_2, y_2) \): Coordinates of the second point
Steps:
- Enter the coordinates of two points.
- Compute rise, run, gradient, angle, and distance.
- Display gradient as a fraction (simplified) or decimal; angle in degrees or radians.
- Format decimal results in scientific notation if the absolute value is less than 0.001 or greater than 10000, otherwise with 4 decimal places.
3. Importance of Gradient Calculation
Calculating these parameters is essential for:
- Geometry: Analyzing slopes and distances.
- Construction: Designing ramps, roads, and roofs.
- Physics: Understanding motion and forces.
- Education: Teaching coordinate geometry concepts.
4. Using the Calculator
Example 1 (Fraction Output): Calculate parameters between two points:
- Point 1: \( (x_1, y_1) = (2, 3) \)
- Point 2: \( (x_2, y_2) = (4, 7) \)
- Gradient Format: Fraction
- Angle Unit: Degrees
- Calculations:
- Rise: \( \Delta y = 7 - 3 = 4 \)
- Run: \( \Delta x = 4 - 2 = 2 \)
- Gradient: \( m = \frac{4}{2} = 2 \)
- Angle: \( \theta = \arctan(2) \approx 63.4349^\circ \)
- Distance: \( d = \sqrt{2^2 + 4^2} = \sqrt{20} \approx 4.4721 \)
- Results:
- Rise: 4.0000
- Run: 2.0000
- Gradient: 2
- Angle: 63.4349
- Distance: 4.4721
Example 2 (Decimal Output): Calculate parameters between two points:
- Point 1: \( (x_1, y_1) = (10, 20) \)
- Point 2: \( (x_2, y_2) = (30, 50) \)
- Gradient Format: Decimal
- Angle Unit: Radians
- Calculations:
- Rise: \( \Delta y = 50 - 20 = 30 \)
- Run: \( \Delta x = 30 - 10 = 20 \)
- Gradient: \( m = \frac{30}{20} = 1.5 \)
- Angle: \( \theta = \arctan(1.5) \approx 0.9828 \, \text{radians} \)
- Distance: \( d = \sqrt{20^2 + 30^2} = \sqrt{1300} \approx 36.0555 \)
- Results:
- Rise: 30.0000
- Run: 20.0000
- Gradient: 1.5000
- Angle: 0.9828
- Distance: 36.0555
5. Frequently Asked Questions (FAQ)
Q: Why is no unit specified?
A: The calculator assumes unitless inputs for simplicity, treating all coordinates as being in the same unit.
Q: Why do I get an error for gradient or angle?
A: If x₁ = x₂, the gradient and angle are undefined due to division by zero.
Q: What if I leave inputs blank?
A: All coordinate fields must be filled with valid numbers to compute results.
 Home
Home
 Back
Back