1. What is a Frustum of a Cone Calculator?

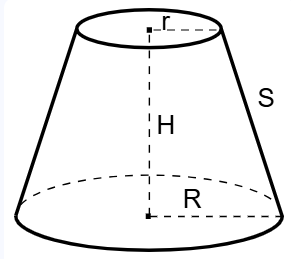
Definition: This calculator computes the slant height (\( S \)) and the total surface area of a conical frustum, given the height (\( H \)), base radius (\( R \)), and top radius (\( r \)). A conical frustum is the portion of a cone between two parallel planes cutting through it, with a larger circular base and a smaller circular top.

Purpose: It aids in geometry education, engineering, and design by providing measurements for frustum-shaped objects, such as buckets, lampshades, or architectural elements.

2. How Does the Calculator Work?

The calculator uses the following formulas:

• Slant height \( S \): \( S = \sqrt{(R - r)^2 + H^2} \).
• Lateral surface area \( A_L \): \( A_L = \pi \cdot (R + r) \cdot S \).
• Top area \( A_{\text{top}} \): \( A_{\text{top}} = \pi \cdot r^2 \).
• Bottom area \( A_{\text{bottom}} \): \( A_{\text{bottom}} = \pi \cdot R^2 \).
• Total surface area \( A \): \( A = A_L + A_{\text{top}} + A_{\text{bottom}} = \pi \cdot (R + r) \cdot S + \pi \cdot r^2 + \pi \cdot R^2 \).

Unit Conversions:

• Length Units: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd).
• Area Units: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²).

Steps:

• Input the height \( H \), base radius \( R \), and top radius \( r \), selecting their units.
• Validate inputs: \( H \) and \( R \) must be positive; \( r \) must be non-negative; \( R \neq r \).
• Convert inputs to meters for calculations.
• Compute the slant height and surface area using the formulas above.
• Convert outputs to the selected units.
• Format outputs to 4 decimal places or scientific notation for small values.

3. Importance of Frustum Calculations

Calculating the properties of a conical frustum is crucial for:

• Geometry Education: Understanding three-dimensional shapes and their properties.
• Engineering and Design: Designing frustum-shaped objects, such as containers, architectural domes, or machine components.
• Manufacturing: Determining material requirements for frustum-shaped structures.

4. Using the Calculator

Examples:

• Example 1: Height \( H = 3 \, \text{cm} \), Base radius \( R = 5 \, \text{cm} \), Top radius \( r = 2 \, \text{cm} \)
  • Convert: \( H = 0.03 \, \text{m} \), \( R = 0.05 \, \text{m} \), \( r = 0.02 \, \text{m} \).
  • Slant height: \( S = \sqrt{(0.05 - 0.02)^2 + 0.03^2} = \sqrt{0.0009 + 0.0009} \approx 0.0424 \, \text{m} = 4.2426 \, \text{cm} \).
  • Lateral surface area: \( A_L = \pi \cdot (0.05 + 0.02) \cdot 0.0424 \approx 0.0093 \, \text{m}^2 \).
  • Top area: \( A_{\text{top}} = \pi \cdot 0.02^2 \approx 0.0013 \, \text{m}^2 \).
  • Bottom area: \( A_{\text{bottom}} = \pi \cdot 0.05^2 \approx 0.0079 \, \text{m}^2 \).
  • Surface area: \( A = 0.0093 + 0.0013 + 0.0079 \approx 0.0185 \, \text{m}^2 = 184.7261 \, \text{cm}^2 \).
• Example 2: Height \( H = 2 \, \text{m} \), Base radius \( R = 3 \, \text{m} \), Top radius \( r = 1 \, \text{m} \)
  • Slant height: \( S = \sqrt{(3 - 1)^2 + 2^2} = \sqrt{4 + 4} \approx 2.8284 \, \text{m} \).
  • Lateral surface area: \( A_L = \pi \cdot (3 + 1) \cdot 2.8284 \approx 35.5437 \, \text{m}^2 \).
  • Top area: \( A_{\text{top}} = \pi \cdot 1^2 \approx 3.1416 \, \text{m}^2 \).
  • Bottom area: \( A_{\text{bottom}} = \pi \cdot 3^2 \approx 28.2743 \, \text{m}^2 \).
  • Surface area: \( A = 35.5437 + 3.1416 + 28.2743 \approx 66.9596 \, \text{m}^2 \).

5. Frequently Asked Questions (FAQ)

Q: What is a conical frustum?
A: A conical frustum is the portion of a cone between two parallel planes, resulting in a shape with a larger circular base (radius \( R \)) and a smaller circular top (radius \( r \)).

Q: Why is the slant height important?
A: The slant height \( S \) is critical for calculating the lateral surface area, which represents the curved surface connecting the top and bottom circles.

Q: Can the top radius be zero?
A: Yes, if \( r = 0 \), the frustum becomes a full cone with the top collapsing to a point (the apex). The calculator supports this case.

Frustum of a Cone Calculator© - All Rights Reserved 2025