Expected Value Calculator

Outcome (x_i)	Probability (P(x_i))

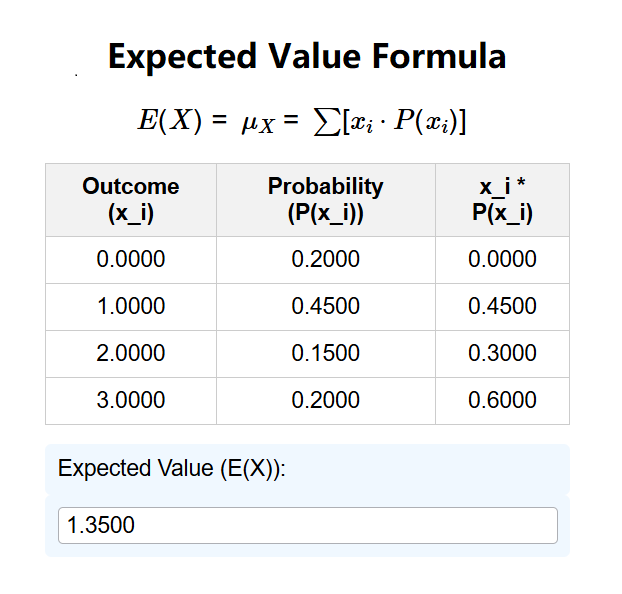
1. What is an Expected Value Calculator?

Definition: This calculator computes the expected value (or mean) of a discrete random variable based on its possible outcomes and their associated probabilities.

Purpose: Helps statisticians, researchers, and decision-makers predict the average outcome of a random event over many trials.

2. How Does the Calculator Work?

The calculator follows these steps:

Step 1: Collect Outcomes and Probabilities

\( x_i \text{ and } P(x_i) \)

Where:

\( x_i \): Possible outcomes of the random variable
\( P(x_i) \): Probability of each outcome, where \( \sum P(x_i) = 1 \)

Step 2: Calculate Expected Value

\( E(X) = \mu_X = \sum [ x_i \cdot P(x_i) ] \)

Where:

\( E(X) \): Expected value (mean) of the random variable
\( x_i \): Each outcome
\( P(x_i) \): Probability of each outcome

Steps:

Enter outcomes and their corresponding probabilities.
Ensure probabilities sum to 1 and are between 0 and 1.
Calculate the expected value by summing the products of outcomes and probabilities.
Display results with 4 decimal places.

3. Importance of Expected Value

Calculating expected value is crucial for:

Decision Making: Evaluates potential outcomes in finance, gambling, and business.
Statistical Analysis: Provides the long-term average of a random variable.
Risk Assessment: Helps balance risk and reward in investments.

4. Using the Calculator

Example 1: Outcomes = 4, 8, 6, 3; Probabilities = 0.1, 0.5, 0.04, 0.36

Verify probabilities: \( 0.1 + 0.5 + 0.04 + 0.36 = 1 \)
Calculate: \( E(X) = (4 \cdot 0.1) + (8 \cdot 0.5) + (6 \cdot 0.04) + (3 \cdot 0.36) \)
\( E(X) = 0.4 + 4 + 0.24 + 1.08 = 5.72 \)
Result: Expected Value = 5.7200

Example 2: Dice roll with outcomes 1 to 6, each with probability \( \frac{1}{6} \)

Calculate: \( E(X) = (1 \cdot \frac{1}{6}) + (2 \cdot \frac{1}{6}) + (3 \cdot \frac{1}{6}) + (4 \cdot \frac{1}{6}) + (5 \cdot \frac{1}{6}) + (6 \cdot \frac{1}{6}) \)
\( E(X) = \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = 3.5 \)
Result: Expected Value = 3.5000

5. Frequently Asked Questions (FAQ)

Q: What if probabilities don’t sum to 1?
A: The calculator will display an error message prompting you to adjust the probabilities.

Q: Can probabilities be negative?
A: No, probabilities must be between 0 and 1, or an error will be shown.

Q: Is expected value always an achievable outcome?
A: No, it’s a theoretical average. For example, a dice roll’s expected value is 3.5, which isn’t a possible outcome.