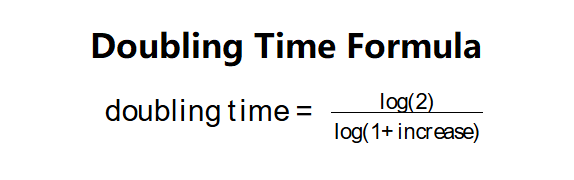Doubling Time Calculator

1. What is the Doubling Time Calculator?

Definition: This calculator determines the time required for a quantity to double in value at a constant growth rate, using the formula \( \text{doubling time} = \frac{\log(2)}{\log(1 + \text{increase})} \), where the increase is the growth rate as a decimal.

Purpose: It assists in understanding exponential growth in fields like finance (e.g., investment growth), biology (e.g., population growth), or physics (e.g., radioactive decay), by calculating how long it takes for a quantity to double.

2. How Does the Calculator Work?

The calculator uses the following equation:

Doubling Time: \( \text{doubling time} = \frac{\log(2)}{\log(1 + \text{increase})} \)

Where:

\( \text{increase} \): Constant growth rate as a decimal (e.g., 5% = 0.05);
\( \text{doubling time} \): Time needed for the quantity to double in value.

Steps:

Enter the constant growth rate as a percentage (e.g., 5 for 5%).
Select the desired time unit (years, months, or days).
The calculator converts the growth rate to a decimal (\( \text{increase} = \frac{\text{growth rate}}{100} \)).
Calculate the doubling time using the formula.
Adjust the result based on the selected time unit (e.g., multiply by 12 for months, 365 for days).
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Doubling Time Calculation

Calculating doubling time is crucial for:

Financial Planning: Estimating how long it takes for investments to double in value.
Population Studies: Understanding growth rates of populations or bacteria.
Resource Management: Predicting when resources might double in demand.
Educational Purposes: Teaching exponential growth concepts.

4. Using the Calculator

Example 1 (Investment Growth): Calculate the doubling time for an investment with a 5% annual growth rate:

Growth Rate: \( 5\% \), so \( \text{increase} = 0.05 \);
Time Unit: Years;
Doubling Time: \( \frac{\log(2)}{\log(1 + 0.05)} = \frac{\log(2)}{\log(1.05)} \approx 14.2067 \);
Result: \( \text{doubling time} = 14.2067 \, \text{years} \).

Example 2 (Population Growth in Days): Calculate the doubling time for a bacterial population with a 2% daily growth rate:

Growth Rate: \( 2\% \), so \( \text{increase} = 0.02 \);
Time Unit: Days;
Doubling Time in Years: \( \frac{\log(2)}{\log(1 + 0.02)} = \frac{\log(2)}{\log(1.02)} \approx 35.0028 \);
Convert to Days: \( 35.0028 \times 365 \approx 12776.0326 \);
Result: \( \text{doubling time} = 12776.0326 \, \text{days} \).

5. Frequently Asked Questions (FAQ)

Q: What happens if the growth rate is zero or negative?
A: The calculator requires a positive growth rate, as a zero or negative rate does not result in doubling (it would lead to no growth or decay).

Q: Can I use this for compound interest?
A: Yes, if the interest compounds continuously, the growth rate can be used to calculate the doubling time of the investment.

Q: How accurate is the result?
A: The result is displayed with 4 decimal places, or in scientific notation if the value is less than 0.001, ensuring high precision.