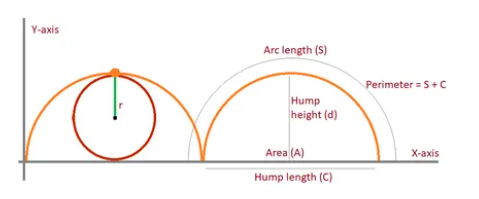
1. What is the Cycloid Calculator?
Definition: This calculator computes properties of a cycloid, which is the curve traced by a point on the rim of a circular wheel as it rolls along a straight line without slipping.
Purpose: It assists in geometry and physics problems involving cycloids, useful in fields like mechanics, animation, and design.
2. How Does the Calculator Work?
The calculator uses the following formulas:
- Area of Cycloid: \( A = 3 \times \pi \times r^2 \)
- Arc Length: \( S = 8 \times r \)
- Hump Height: \( d = 2 \times r \)
- Hump Length: \( C = 2 \times \pi \times r \)
- Perimeter of Cycloid: \( p = C + S \)
Steps:
- Enter the radius of the rolling circle along with its unit (mm, cm, m, in, ft, or yd).
- Convert the radius to meters for calculation.
- Compute the cycloid properties in meters (for lengths) and square meters (for area).
- Convert each result to its selected output unit independently.
- Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Cycloid Calculations
Calculating cycloid properties is essential for:
Mechanics: Understanding motion in systems like gears and pendulums (e.g., the brachistochrone problem).
Design: Creating smooth curves in architecture and engineering.
Animation: Simulating realistic rolling motion in graphics.
Education: Studying parametric equations and geometric curves.
4. Using the Calculator
Example 1: Calculate the cycloid properties:
- Radius: \( r = 5 \, \text{in} \);
- Output Units: Area in in², Lengths in in;
- Convert to meters: \( r = 5 \times 0.0254 = 0.127 \, \text{m} \);
- Area in m²: \( A = 3 \times \pi \times r^2 = 3 \times \pi \times (0.127)^2 \approx 0.151745 \, \text{m}^2 \);
- Arc Length in m: \( S = 8 \times r = 8 \times 0.127 = 1.016 \, \text{m} \);
- Hump Height in m: \( d = 2 \times r = 2 \times 0.127 = 0.254 \, \text{m} \);
- Hump Length in m: \( C = 2 \times \pi \times r = 2 \times \pi \times 0.127 \approx 0.797965 \, \text{m} \);
- Perimeter in m: \( p = C + S \approx 0.797965 + 1.016 = 1.813965 \, \text{m} \);
- Convert to in and in²: \( A = 0.151745 \div 0.00064516 \approx 235.1123 \, \text{in}^2 \), \( S = 1.016 \div 0.0254 = 40 \, \text{in} \), \( d = 0.254 \div 0.0254 = 10 \, \text{in} \), \( C = 0.797965 \div 0.0254 \approx 31.4159 \, \text{in} \), \( p = 1.813965 \div 0.0254 \approx 71.4159 \, \text{in} \);
- Results: \( A = 235.1123 \, \text{in}^2 \), \( S = 40.0000 \, \text{in} \), \( d = 10.0000 \, \text{in} \), \( C = 31.4159 \, \text{in} \), \( p = 71.4159 \, \text{in} \).
Example 2: Calculate the cycloid properties:
- Radius: \( r = 2 \, \text{in} \);
- Output Units: Area in in², Arc Length in cm, Hump Height in in, Hump Length in ft, Perimeter in yd;
- Convert to meters: \( r = 2 \times 0.0254 = 0.0508 \, \text{m} \);
- Area in m²: \( A = 3 \times \pi \times r^2 = 3 \times \pi \times (0.0508)^2 \approx 0.024321 \, \text{m}^2 \);
- Arc Length in m: \( S = 8 \times r = 8 \times 0.0508 = 0.4064 \, \text{m} \);
- Hump Height in m: \( d = 2 \times r = 2 \times 0.0508 = 0.1016 \, \text{m} \);
- Hump Length in m: \( C = 2 \times \pi \times r = 2 \times \pi \times 0.0508 \approx 0.319186 \, \text{m} \);
- Perimeter in m: \( p = C + S \approx 0.319186 + 0.4064 = 0.725586 \, \text{m} \);
- Convert results: \( A = 0.024321 \div 0.00064516 \approx 37.6991 \, \text{in}^2 \), \( S = 0.4064 \times 100 = 40.64 \, \text{cm} \), \( d = 0.1016 \div 0.0254 = 4 \, \text{in} \), \( C = 0.319186 \div 0.3048 \approx 1.0472 \, \text{ft} \), \( p = 0.725586 \div 0.9144 \approx 0.7935 \, \text{yd} \);
- Results: \( A = 37.6991 \, \text{in}^2 \), \( S = 40.6400 \, \text{cm} \), \( d = 4.0000 \, \text{in} \), \( C = 1.0472 \, \text{ft} \), \( p = 0.7935 \, \text{yd} \).
5. Frequently Asked Questions (FAQ)
Q: What is a cycloid?
A: A cycloid is the curve traced by a point on the rim of a circular wheel as it rolls along a straight line without slipping.
Q: Why can I choose different units for each result?
A: Independent unit selection allows flexibility for users working with mixed unit systems in practical applications.
Q: Can I use this calculator for other curves?
A: No, this calculator is specifically designed for cycloids. Other curves like epicycloids or hypocycloids require different formulas.
 Home
Home
 Back
Back