Cotangent (Cot) Calculator

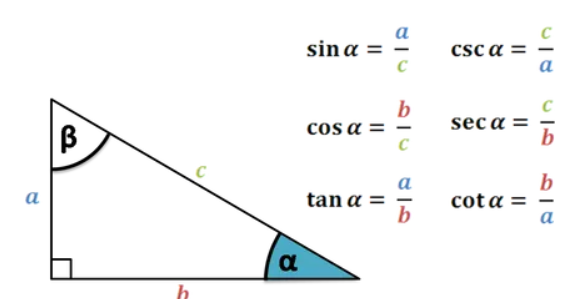
1. What is the Cotangent (Cot) Calculator?

Definition: This calculator computes the cotangent (\( \cot(x) \)) of a given angle \( x \), where \( \cot(x) = \frac{1}{\tan(x)} \).

Purpose: It is used in trigonometry to analyze reciprocal relationships of angles, often in geometry, physics, and engineering problems.

2. How Does the Calculator Work?

The calculator uses the following definition of cotangent:

\( \cot(x) = \frac{1}{\tan(x)} \)
Alternatively: \( \cot(x) = \frac{\cos(x)}{\sin(x)} \)

Where:

\( x \): The input angle in various units
\( \tan(x) \): The tangent of the angle

Unit Conversions (Input Angle):

Angle (\( x \)):
- Degrees (deg): Directly input in degrees
- Radians (rad): Directly input in radians
- Gradians (gon): \( \text{rad} = \text{gon} \times \frac{\pi}{200} \)
- Turns (tr): \( \text{rad} = \text{tr} \times 2\pi \)
- Minutes of Arc (arcmin): \( \text{rad} = \text{deg2rad}(\text{arcmin} / 60) \)
- Seconds of Arc (arcsec): \( \text{rad} = \text{deg2rad}(\text{arcsec} / 3600) \)
- Milliradians (mrad): \( \text{rad} = \text{mrad} / 1000 \)
- Microradians (urad): \( \text{rad} = \text{urad} / 1000000 \)
- π Radians (x π rad): \( \text{rad} = \text{x π rad} \times \pi \)

Steps:

Enter the angle \( x \) and select its unit (e.g., deg, rad).
Click "Calculate" to compute \( \cot(x) = \frac{1}{\tan(x)} \).
The result is displayed with 4 decimal places.

3. Importance of Cotangent Calculation

Calculating the cotangent is crucial for:

Trigonometry: Understanding reciprocal relationships in right triangles and unit circles.
Physics: Analyzing wave properties, oscillations, and periodic motion.
Engineering: Solving problems in signal processing, control systems, and structural analysis.

4. Using the Calculator

Example: Calculate the cotangent of \( x = 30^\circ \).

Enter \( x = 30 \) and select the unit as "deg".
Click "Calculate" to compute:
- \( \tan(30^\circ) = \frac{\sqrt{3}}{3} \approx 0.5774 \)
- \( \cot(30^\circ) = \frac{1}{\tan(30^\circ)} = \sqrt{3} \approx 1.7321 \)

5. Frequently Asked Questions (FAQ)

Q: What is the cotangent (cot)?
A: The cotangent (\( \cot(x) \)) is the reciprocal of the tangent function, defined as \( \cot(x) = \frac{1}{\tan(x)} \), or equivalently \( \cot(x) = \frac{\cos(x)}{\sin(x)} \).

Q: When is cotangent undefined?
A: Cotangent is undefined when \( \tan(x) = 0 \), which occurs at angles like \( 0^\circ \), \( 180^\circ \), \( 360^\circ \), etc. (or equivalent in other units).

Q: What are the different angle units?
A: Angles can be measured in various units:

Degrees (deg): 360° in a full circle.
Radians (rad): \( 2\pi \) in a full circle.
Gradians (gon): 400 gon in a full circle.
Turns (tr): 1 turn is a full circle.
Minutes of Arc (arcmin): 60 arcmin per degree.
Seconds of Arc (arcsec): 3600 arcsec per degree.
Milliradians (mrad): 1000 mrad per radian.
Microradians (urad): 1000000 urad per radian.
π Radians (x π rad): Expressed as a multiple of π.