1. What is the Conic Sections Calculator?

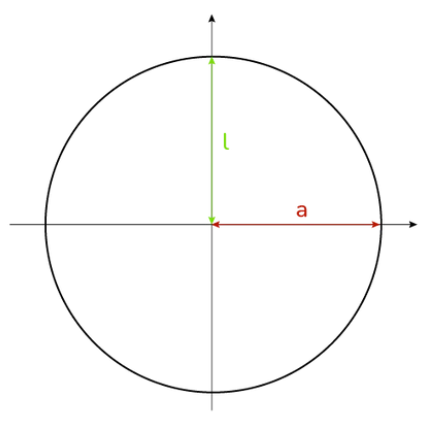
Definition: This calculator computes the parameters of various conic sections (Circle, Ellipse, Parabola, Hyperbola) based on their defining parameters.

Purpose: It assists in geometry and engineering problems involving conic sections, useful in fields like astronomy, optics, and structural design.

2. How Does the Calculator Work?

The calculator uses the following equation for the selected conic shape:

• Circle: \( x^2 + y^2 = a^2 \)

Computed Parameters:

• Eccentricity (\( e \))
• Linear Eccentricity (\( c \))
• Semi-latus Rectum (\( l \))

Calculation Formulas:

• Eccentricity: \( e = 0 \)
• Linear Eccentricity: \( c = 0 \)
• Semi-latus Rectum: \( l = a \)

Steps:

• Select the conic shape from the dropdown menu.
• Enter the required parameters (e.g., radius for a circle, semi-major and semi-minor axes for an ellipse).
• Compute the conic parameters based on the shape-specific formulas.
• Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

Conic Section	Equation	Eccentricity (e)	Linear Eccentricity (c)	Semi Latus Rectum (l)
Circle	x2 + y2 = a2	0	0	a
Ellipse (horizontal)	x2⁄a2 + y2⁄b2 = 1	√(1 - b2⁄a2)	√(a2 - b2)	b2⁄a
Ellipse (vertical)	x2⁄b2 + y2⁄a2 = 1	√(1 - b2⁄a2)	√(a2 - b2)	b2⁄a
Parabola	y2 = 4ax	1	NaN	2a
Hyperbola (horizontal)	x2⁄a2 - y2⁄b2 = 1	√(1 + b2⁄a2)	√(a2 + b2)	b2⁄a
Hyperbola (vertical)	-x2⁄a2 + y2⁄b2 = 1	√(1 + a2⁄b2)	√(b2 + a2)	a2⁄b

3. Importance of Conic Sections Calculations

Calculating conic parameters is essential for:

Astronomy: Modeling planetary orbits (ellipses, hyperbolas). Optics: Designing lenses and mirrors (parabolas, ellipses). Engineering: Analyzing structural shapes and trajectories. Geometry Education: Understanding fundamental properties of conic sections.

4. Using the Calculator

Example 1 (Circle): Calculate the parameters of a circle:

• Radius: \( a = 15 \);
• Eccentricity: \( e = 0 \);
• Linear Eccentricity: \( c = 0 \);
• Semi-latus Rectum: \( l = a = 15 \);
• Result: \( e = 0.0000 \), \( c = 0.0000 \), \( l = 15.0000 \).

Example 2 (Ellipse Horizontal): Calculate the parameters of an ellipse:

• Semi-major Axis: \( a = 12 \);
• Semi-minor Axis: \( b = 5 \);
• Eccentricity: \( e = \sqrt{1 - \frac{b^2}{a^2}} = \sqrt{1 - \frac{5^2}{12^2}} = \sqrt{1 - \frac{25}{144}} = \sqrt{\frac{119}{144}} \approx 0.9099 \);
• Linear Eccentricity: \( c = \sqrt{a^2 - b^2} = \sqrt{12^2 - 5^2} = \sqrt{144 - 25} = \sqrt{119} \approx 10.9087 \);
• Semi-latus Rectum: \( l = \frac{b^2}{a} = \frac{5^2}{12} = \frac{25}{12} \approx 2.0833 \);
• Result: \( e = 0.9099 \), \( c = 10.9087 \), \( l = 2.0833 \).

5. Frequently Asked Questions (FAQ)

Q: What is the difference between horizontal and vertical ellipses/hyperbolas?
A: Horizontal ellipses/hyperbolas have the larger axis along the x-axis (\( a > b \)), while vertical ones have the larger axis along the y-axis.

Q: Why is the linear eccentricity not defined for a parabola?
A: A parabola's eccentricity is 1, and it does not have a second focus, so the linear eccentricity is not defined.

Q: What if I enter negative values?
A: The calculator will display an error, as all input parameters must be positive.

Conic Sections Calculator© - All Rights Reserved 2025