Complex Conjugate Calculator

1. What is the Conjugate? The Conjugate Definition

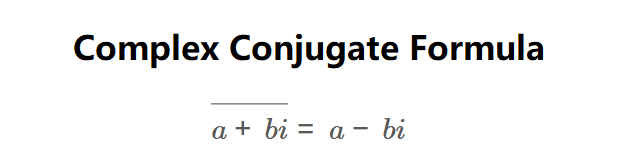
Let’s start with the conjugate definition because it’s so simple.

The conjugate of a complex number \( z = a + bi \) is the number \( a - bi \). We denote this operation by putting a horizontal line over the value like this:

\( \overline{a + bi} = a - bi \)

It may seem like the conjugate in math is a simple, useless operation that doesn’t change much. In fact, the conjugate of a number has a deeper meaning that we’ll try to explain in a second.

Do you know how we mark real numbers on a line? With complex numbers, it’s not that easy because we don’t know if \( i \) is smaller or larger than 0 (in fact, it’s neither). Therefore, we need two axes to describe them, which together form the complex plane.

2. Importance of Complex Conjugates

Complex conjugates are essential for:

Rationalization: Simplifying fractions with complex denominators by making the denominator real.
Signal Processing: Modeling wave functions and harmonic motion, where conjugates help compute magnitudes.
Geometry: Representing reflections in the complex plane, useful in physics and engineering.

3. Using the Calculator

Example 1: Find the conjugate of \( 5 + 2i \):

Inputs: \( a = 5 \), \( b = 2 \);
Conjugate: \( 5 - 2i \);
Absolute value: \( \sqrt{5^2 + 2^2} = \sqrt{29} \approx 5.3852 \).

Example 2: Find the conjugate of \( 3 - 4i \):

Inputs: \( a = 3 \), \( b = -4 \);
Conjugate: \( 3 + 4i \);
Absolute value: \( \sqrt{3^2 + (-4)^2} = \sqrt{25} = 5 \).

Example 3: Find the conjugate of \( 7 \):

Inputs: \( a = 7 \), \( b = 0 \);
Conjugate: \( 7 \);
Absolute value: \( \sqrt{7^2 + 0^2} = 7 \).

4. Frequently Asked Questions (FAQ)

Q: What is a complex conjugate?
A: It’s a complex number with the same real part but the opposite imaginary part, e.g., the conjugate of \( a + bi \) is \( a - bi \).

Q: What is the absolute value of a complex number?
A: The absolute value of \( a + bi \) is \( \sqrt{a^2 + b^2} \), representing the distance from the origin in the complex plane.

Q: How is the conjugate used in real-world applications?
A: It’s used in signal processing to compute magnitudes of complex wave functions and in electrical engineering to simplify circuit analysis.