Chord Length Calculator

Radius (r):

Central Angle (α):

Chord Length (c):

Chord Height (h):

Apothem (r - h):

1. What is the Chord Length Calculator?

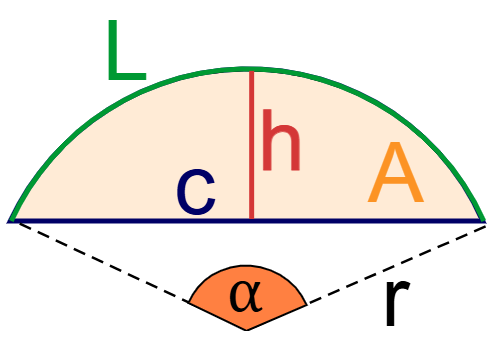
Definition: This calculator computes the chord length, chord height, and apothem of a circle given the radius \( r \) and central angle \( \alpha \).

Purpose: It assists in geometry problems involving circular segments, useful in fields like engineering, architecture, and mathematics.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Chord Length: \( c = 2 \times r \times \sin(\alpha / 2) \)
Chord Height: \( h = r \times (1 - \cos(\alpha / 2)) \)
Apothem: \( r - h \)

Where:

\( r \): Radius of the circle (mm, cm, m, in, ft, or yd);
\( \alpha \): Central angle (degrees or radians);
\( c \): Chord length (mm, cm, m, in, ft, or yd);
\( h \): Chord height (mm, cm, m, in, ft, or yd);
\( r - h \): Apothem, distance from the center to the chord (mm, cm, m, in, ft, or yd).

Steps:

Enter the radius \( r \) and central angle \( \alpha \) along with their units (radius: mm, cm, m, in, ft, yd; angle: degrees or radians).
Convert the radius to meters and the angle to radians if necessary.
Calculate the chord length using \( c = 2 \times r \times \sin(\alpha / 2) \).
Calculate the chord height using \( h = r \times (1 - \cos(\alpha / 2)) \).
Calculate the apothem as \( r - h \).
Convert results to the selected output unit (mm, cm, m, in, ft, or yd).
Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Chord Length Calculations

Calculating the chord length, height, and apothem is essential for:

Engineering:

Architecture:

Geometry Education:

Physics:

4. Using the Calculator

Example 1 (Metric Units): Calculate the chord length, height, and apothem:

Radius: \( r = 5 \, \text{m} \);
Central Angle: \( \alpha = 60^\circ \);
Output Unit: Meters (m);
Convert angle: \( \alpha = 60 \times \frac{\pi}{180} = \frac{\pi}{3} \, \text{radians} \);
Chord Length: \( c = 2 \times 5 \times \sin\left(\frac{\pi/3}{2}\right) = 10 \times \sin(\pi/6) = 10 \times 0.5 = 5 \, \text{m} \);
Chord Height: \( h = 5 \times (1 - \cos(\pi/6)) = 5 \times (1 - \sqrt{3}/2) \approx 5 \times (1 - 0.8660) \approx 0.6700 \, \text{m} \);
Apothem: \( r - h = 5 - 0.6700 \approx 4.3300 \, \text{m} \);
Result: \( c = 5.0000 \, \text{m} \), \( h = 0.6700 \, \text{m} \), \( r - h = 4.3300 \, \text{m} \).

Example 2 (Mixed Units): Calculate the chord length, height, and apothem:

Radius: \( r = 10 \, \text{ft} \);
Central Angle: \( \alpha = \frac{\pi}{4} \, \text{radians} \);
Output Unit: Feet (ft);
Convert radius: \( r = 10 \times 0.3048 = 3.048 \, \text{m} \);
Chord Length: \( c = 2 \times 3.048 \times \sin\left(\frac{\pi/4}{2}\right) = 6.096 \times \sin(\pi/8) \approx 6.096 \times 0.3827 \approx 2.3330 \, \text{m} \approx 7.6542 \, \text{ft} \);
Chord Height: \( h = 3.048 \times (1 - \cos(\pi/8)) \approx 3.048 \times (1 - 0.9239) \approx 0.2319 \, \text{m} \approx 0.7608 \, \text{ft} \);
Apothem: \( r - h = 3.048 - 0.2319 \approx 2.8161 \, \text{m} \approx 9.2392 \, \text{ft} \);
Result: \( c = 7.6542 \, \text{ft} \), \( h = 0.7608 \, \text{ft} \), \( r - h = 9.2392 \, \text{ft} \).

5. Frequently Asked Questions (FAQ)

Q: What if the central angle is 0 or 2π?
A: If the angle is 0, the chord length is 0. If the angle is 2π (or 360°), it represents a full circle, and the chord length is the diameter, but the calculator will display an error as the angle must be less than 2π.

Q: Can I use degrees instead of radians?
A: Yes, the calculator allows you to input the angle in degrees or radians, converting internally as needed.

Q: Why are chord height and apothem calculated?
A: These values provide additional geometric information about the circular segment, useful for design and analysis.