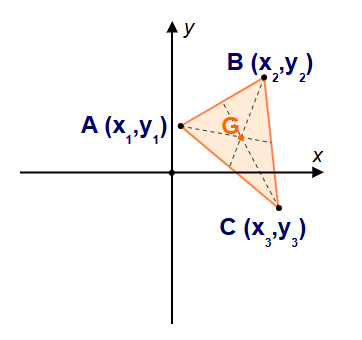
1. What is the Centroid Calculator?
Definition: This calculator computes the centroid (center of mass) of a triangle given the coordinates of its three vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \). It also calculates the area of the triangle.
Purpose: It assists students, engineers, and designers in finding the centroid and area of a triangle for applications in geometry, physics, and structural analysis.
2. How Does the Calculator Work?
The calculator uses the following formulas:
- Centroid: \( G = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) \)
- Area: \( A = \frac{1}{2} \left| x_1 (y_2 - y_3) + x_2 (y_3 - y_1) + x_3 (y_1 - y_2) \right| \)
Where:
- \( (x_1, y_1) \), \( (x_2, y_2) \), \( (x_3, y_3) \): Coordinates of vertices A, B, and C (mm, cm, m, in, ft, or yd);
- \( G \): Centroid coordinates (mm, cm, m, in, ft, or yd);
- \( A \): Area of the triangle (mm², cm², m², in², ft², or yd²).
Steps:
- Enter the coordinates of vertices A, B, and C along with their units (mm, cm, m, in, ft, or yd).
- Convert all coordinates to SI units (meters).
- Calculate the area using the shoelace formula to ensure the points form a triangle (area ≠ 0).
- Calculate the centroid coordinates by averaging the x and y coordinates.
- Convert the centroid coordinates and area to the selected output units.
- Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Centroid Calculations
Calculating the centroid and area of a triangle is essential for:
Physics: Determines the center of mass for stability analysis.
Engineering: Used in structural design to find balance points.
Geometry Education: Teaches fundamental concepts of triangle properties.
Computer Graphics: Assists in rendering and manipulating triangular shapes.
4. Using the Calculator
Example 1 (Metric Units): Calculate the centroid and area of a triangle:
- Vertex A: \( (1, 1) \, \text{m} \);
- Vertex B: \( (3, 4) \, \text{m} \);
- Vertex C: \( (5, 1) \, \text{m} \);
- Centroid Output Unit: Meters (m);
- Area Output Unit: Square Meters (m²);
- Centroid: \( G_x = \frac{1+3+5}{3} = 3 \), \( G_y = \frac{1+4+1}{3} = 2 \), so \( G = (3, 2) \, \text{m} \);
- Area: \( A = \frac{1}{2} \left| 1(4-1) + 3(1-1) + 5(1-4) \right| = \frac{1}{2} \left| 3 + 0 - 15 \right| = \frac{1}{2} \cdot 12 = 6 \, \text{m}^2 \);
- Result: \( G = (3.0000, 2.0000) \, \text{m} \), \( A = 6.0000 \, \text{m}^2 \).
Example 2 (Mixed Units): Calculate the centroid and area of a triangle:
- Vertex A: \( (0, 0) \, \text{ft} \);
- Vertex B: \( (3, 0) \, \text{ft} \);
- Vertex C: \( (0, 4) \, \text{ft} \);
- Centroid Output Unit: Feet (ft);
- Area Output Unit: Square Yards (yd²);
- Convert to SI: \( (0, 0) \, \text{m} \), \( (3 \times 0.3048, 0) = (0.9144, 0) \, \text{m} \), \( (0, 4 \times 0.3048) = (0, 1.2192) \, \text{m} \);
- Centroid: \( G_x = \frac{0+0.9144+0}{3} \approx 0.3048 \, \text{m} \), \( G_y = \frac{0+0+1.2192}{3} \approx 0.4064 \, \text{m} \);
- Centroid in ft: \( G_x = 0.3048 \div 0.3048 = 1.0000 \, \text{ft} \), \( G_y = 0.4064 \div 0.3048 \approx 1.3333 \, \text{ft} \);
- Area: \( A = \frac{1}{2} \left| 0(0-1.2192) + 0.9144(1.2192-0) + 0(0-0) \right| = \frac{1}{2} \cdot 0.9144 \cdot 1.2192 \approx 0.5574 \, \text{m}^2 \);
- Area in yd²: \( 0.5574 \div 0.836127 \approx 0.6667 \, \text{yd}^2 \);
- Result: \( G = (1.0000, 1.3333) \, \text{ft} \), \( A = 0.6667 \, \text{yd}^2 \).
5. Frequently Asked Questions (FAQ)
Q: What happens if the points are collinear?
A: If the points lie on a straight line (area = 0), they do not form a triangle, and the calculator will display an error.
Q: Can I use different units for each vertex?
A: Yes, the calculator allows independent unit selection for each vertex's coordinates.
Q: Why is the area calculated?
A: The area is calculated to validate that the points form a triangle and to provide additional useful information about the shape.
 Home
Home
 Back
Back