Ceiling Function Calculator

1. What is the Ceiling Function Calculator?

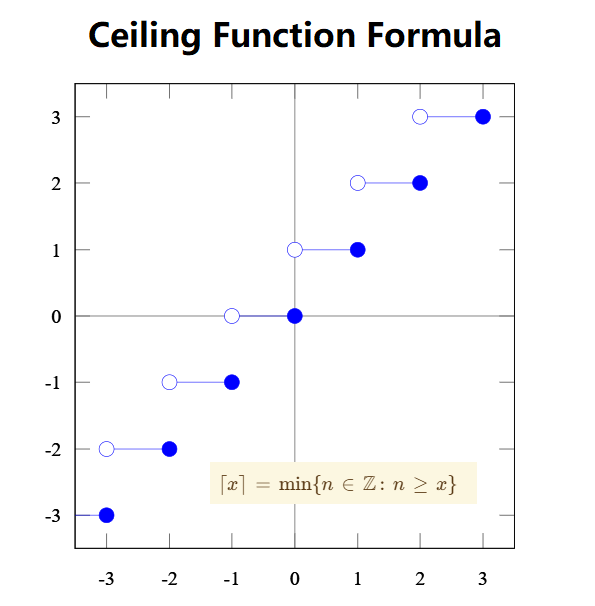
Definition: This calculator computes the ceiling value of a number, which is the smallest integer greater than or equal to the input number, denoted as \( \lceil x \rceil \).

Purpose: It helps students, programmers, and professionals quickly determine the ceiling value of any number, useful in mathematics, computer science, and real-world applications.

2. How Does the Calculator Work?

The calculator uses the ceiling function:

\[ \lceil x \rceil \]

Where:

\( x \): The input number;
\( \lceil x \rceil \): The smallest integer greater than or equal to \( x \). For example, \( \lceil 3.2 \rceil = 4 \), \( \lceil -2.7 \rceil = -2 \).

Steps:

Enter the number (\( x \)).
Calculate the ceiling value using the ceiling function.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of the Ceiling Function

The ceiling function is crucial for:

Mathematics: Used in number theory, rounding, and solving inequalities.
Computer Science: Essential in algorithms for tasks like memory allocation, array indexing, or dividing tasks into whole units.
Finance: Helps in rounding up prices or quantities to the nearest whole unit (e.g., number of items to order).
Everyday Use: Useful in scenarios like determining the number of boxes needed to pack items, where partial units require an extra box.

4. Using the Calculator

Example 1 (Positive Decimal): Calculate the ceiling of a positive decimal number:

Input Number: \( x = 3.7 \);
Ceiling Value: \( \lceil 3.7 \rceil = 4 \);
Result: \( 4.0000 \).

Example 2 (Negative Decimal): Calculate the ceiling of a negative decimal number:

Input Number: \( x = -2.3 \);
Ceiling Value: \( \lceil -2.3 \rceil = -2 \);
Result: \( -2.0000 \).

5. Frequently Asked Questions (FAQ)

Q: How is the ceiling function different from rounding?
A: The ceiling function always rounds up to the next integer, regardless of the decimal part, while rounding typically rounds to the nearest integer (e.g., \( \text{round}(3.7) = 4 \), but \( \text{round}(3.4) = 3 \)).

Q: What happens if the input is an integer?
A: If the input is an integer, the ceiling value is the same as the input (e.g., \( \lceil 5 \rceil = 5 \)).

Q: How does the ceiling function handle negative numbers?
A: For negative numbers, the ceiling function rounds to the nearest integer greater than the number (e.g., \( \lceil -2.3 \rceil = -2 \), not \(-3\)).