Binomial Coefficient Calculator

1. What is a Binomial Coefficient Calculator?

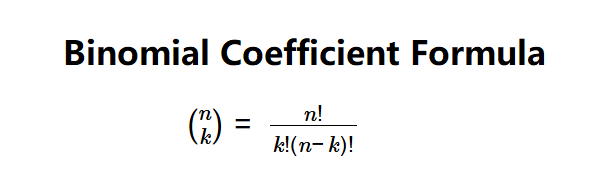
Definition: This calculator computes the binomial coefficient $(\binom{n}{k})$ , which represents the number of ways to choose $k$ items from $n$ items without regard to order. It’s also known as "n choose k."

Purpose: It helps in probability, combinatorics, and algebra, such as calculating combinations, expanding binomials, or constructing Pascal’s triangle.

2. How Does the Calculator Work?

The calculator uses the binomial coefficient formula:

$(\binom{n}{k}) = \frac{n!}{k! (n - k)!}$
If $k < 0$ or $k > n$ , then $(\binom{n}{k}) = 0$ .
Optimizes computation by using the smaller of $k$ or $n - k$ to reduce the number of multiplications.

Where:

$n$ : Total number of items;
$k$ : Number of items to choose;
$n!$ : Factorial of $n$ , i.e., $n \times (n - 1) \times \dots \times 1$ ;
Results are integers, as binomial coefficients are counts.

Properties of Binomial Coefficients

Property	Description
Symmetry	$(\binom{n}{k}) = (\binom{n}{n - k})$
Base Cases	$(\binom{n}{0}) = (\binom{n}{n}) = 1$
Invalid Cases	$(\binom{n}{k}) = 0$ if $k < 0$ or $k > n$

Notes:

Computation is limited to $n \leq 1000$ to prevent overflow.
Inputs must be non-negative integers.

Steps to Use:

Enter $n$ (total items) and $k$ (items to choose).
Click "Calculate" to compute $(\binom{n}{k})$ .
View the result, which is the number of combinations.

3. Importance of Binomial Coefficients

Binomial coefficients are essential for:

Combinatorics: Calculating the number of ways to choose items (e.g., lottery odds).
Binomial Theorem: Expanding expressions like $(x + y)^{n}$ .
Pascal’s Triangle: Each entry in the triangle is a binomial coefficient.

4. Using the Calculator

Example 1: Compute $(\binom{5}{2})$ :

Inputs: $n = 5$ , $k = 2$ ;
Formula: $(\binom{5}{2}) = \frac{5!}{2! (5 - 2)!} = \frac{5 \times 4}{2 \times 1} = 10$ ;
Result: 10.

Example 2: Compute $(\binom{6}{4})$ :

Inputs: $n = 6$ , $k = 4$ ;
Formula: $(\binom{6}{4}) = (\binom{6}{2}) = \frac{6 \times 5}{2 \times 1} = 15$ ;
Result: 15.

Example 3: Compute $(\binom{3}{5})$ :

Inputs: $n = 3$ , $k = 5$ ;
Since $k > n$ , the result is 0;
Result: 0.

5. Frequently Asked Questions (FAQ)

Q: What does $(\binom{n}{k})$ represent?
A: It represents the number of ways to choose $k$ items from $n$ items without regard to order.

Q: Why is the result 0 when $k > n$ ?
A: You cannot choose more items than are available, so the number of combinations is 0.

Q: How are binomial coefficients related to Pascal’s triangle?
A: Each entry in Pascal’s triangle is a binomial coefficient, where row $n$ , position $k$ is $(\binom{n}{k})$ .