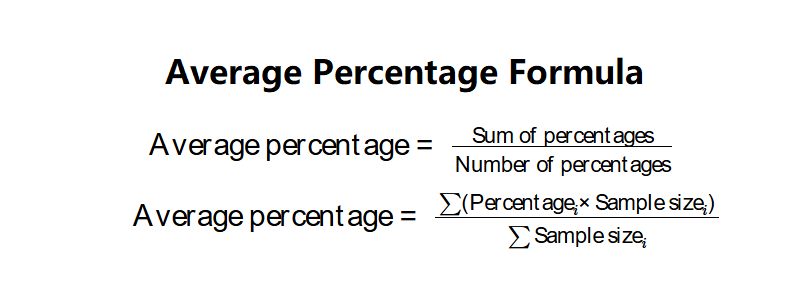Average Percentage Calculator

Use Sample Sizes (Weighted Average):

Percentage 1 (%):

Percentage 2 (%):

1. What is Average Percentage Calculator?

Definition: This calculator computes the average percentage from a set of percentage values, either as a simple average or a weighted average based on sample sizes.

Purpose: It is used in statistics, education, and data analysis to find the mean percentage across multiple datasets, such as survey results, test scores, or poll percentages.

2. How Does the Calculator Work?

The calculator uses the following equations:

Simple Average: \( \text{Average percentage} = \frac{\text{Sum of percentages}}{\text{Number of percentages}} \)
Weighted Average: \( \text{Average percentage} = \frac{\sum (\text{Percentage}_i \times \text{Sample size}_i)}{\sum \text{Sample size}_i} \)

Steps:

Start with 2 percentage input fields (add more if needed, up to 10).
Enter percentage values (between 0 and 100).
Check the box to use sample sizes for a weighted average if desired.
If using sample sizes, enter the sample size for each percentage (must be positive).
Collect all valid percentage values (and sample sizes if applicable).
Calculate the average:
- For simple average: Sum the percentages and divide by the count.
- For weighted average: Multiply each percentage by its sample size, sum the results, and divide by the total sample size.
Display the result: average percentage, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Average Percentage Calculation

Calculating the average percentage is crucial for:

Survey Analysis: Determines the overall percentage response across multiple groups.
Educational Assessment: Averages test scores or grades across different classes or subjects.
Data Representation: Provides a single representative percentage for datasets with varying sample sizes.

4. Using the Calculator

Example 1 (Simple Average): Calculate the average percentage:

Percentages: 60%, 70%;
Sum: \( 60 + 70 = 130 \);
Count: 2;
Average: \( \frac{130}{2} = 65 \);
Result: Average Percentage = 65.0000 %.

Example 2 (Weighted Average): Calculate the average percentage with sample sizes:

Percentages: 60%, 70%;
Sample Sizes: 100, 200;
Weighted Sum: \( (60 \times 100) + (70 \times 200) = 6000 + 14000 = 20000 \);
Total Sample Size: \( 100 + 200 = 300 \);
Average: \( \frac{20000}{300} \approx 66.6667 \);
Result: Average Percentage = 66.6667 %.

5. Frequently Asked Questions (FAQ)

Q: When should I use a weighted average?
A: Use a weighted average when the percentages represent groups of different sizes, such as survey responses from different sample sizes, to ensure the result reflects the sample proportions accurately.

Q: Why can’t I enter percentages greater than 100?
A: Percentages are typically between 0 and 100. Values outside this range may not be meaningful in most contexts for averaging percentages.

Q: What if I don’t enter sample sizes for a weighted average?
A: The calculator requires sample sizes for a weighted average. If a sample size is missing or invalid, that percentage will be ignored unless you switch to a simple average.