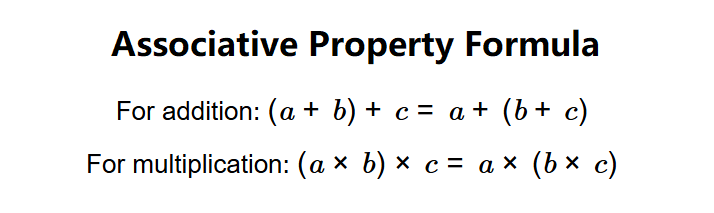Associative Property Calculator

First Number (a):

Second Number (b):

Third Number (c):

Operation:

1. What is the Associative Property Calculator?

Definition: This calculator demonstrates the associative property of addition or multiplication, showing that the grouping of numbers does not affect the result of the operation.

Purpose: It helps students, educators, and math enthusiasts understand and verify the associative property by computing the same operation in two different groupings.

2. How Does the Calculator Work?

The calculator demonstrates the associative property with the following equations:

For addition: \( (a + b) + c = a + (b + c) \)
For multiplication: \( (a \times b) \times c = a \times (b \times c) \)

Where:

\( a \), \( b \), \( c \): The three numbers input by the user;
The left side computes \( (a \text{ op } b) \text{ op } c \), and the right side computes \( a \text{ op } (b \text{ op } c) \).

Steps:

Enter the first number (\( a \)).
Enter the second number (\( b \)).
Enter the third number (\( c \)).
Select the operation (addition or multiplication).
Calculate the result in two ways: \( (a \text{ op } b) \text{ op } c \) and \( a \text{ op } (b \text{ op } c) \).
Display both results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of the Associative Property

The associative property is crucial for:

Mathematics Education: Teaches fundamental properties of operations, aiding in understanding algebraic manipulations.
Simplification: Allows regrouping of terms to make calculations easier (e.g., adding \( (2 + 8) + 5 \) as \( 10 + 5 \)).
Programming: Ensures consistent results in algorithms regardless of operation grouping.
Real-World Applications: Useful in budgeting, combining quantities, or scaling measurements where grouping doesn’t affect the outcome.

4. Using the Calculator

Example 1 (Addition): Verify the associative property for addition:

First Number: \( a = 3 \);
Second Number: \( b = 5 \);
Third Number: \( c = 7 \);
Operation: Addition;
Left: \( (3 + 5) + 7 = 8 + 7 = 15 \);
Right: \( 3 + (5 + 7) = 3 + 12 = 15 \);
Result: Both equal \( 15.0000 \).

Example 2 (Multiplication): Verify the associative property for multiplication:

First Number: \( a = 2 \);
Second Number: \( b = 4 \);
Third Number: \( c = 6 \);
Operation: Multiplication;
Left: \( (2 \times 4) \times 6 = 8 \times 6 = 48 \);
Right: \( 2 \times (4 \times 6) = 2 \times 24 = 48 \);
Result: Both equal \( 48.0000 \).

5. Frequently Asked Questions (FAQ)

Q: Does the associative property apply to subtraction or division?
A: No, the associative property holds only for addition and multiplication. For example, \( (8 - 3) - 2 \neq 8 - (3 - 2) \).

Q: Why are the two results always the same?
A: The associative property guarantees that for addition and multiplication, the grouping of numbers does not change the final result, making operations more flexible.

Q: Can this calculator handle decimal numbers?
A: Yes, the calculator works with decimal numbers, ensuring accurate results for both groupings.