Area of a Rectangle Calculator

Length (a):

Width (b):

Area (A):

Perimeter (P):

Diagonal (d):

1. What is the Area of a Rectangle Calculator?

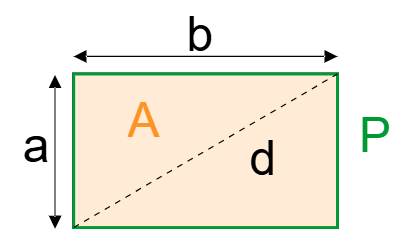
Definition: This calculator computes the area, perimeter, and diagonal of a rectangle based on its length (a) and width (b).

Purpose: It assists students, engineers, and designers in calculating key geometric properties of a rectangle for applications in architecture, design, and mathematics.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Area: \( A = a \times b \)
Perimeter: \( P = 2 \times (a + b) \)
Diagonal: \( d = \sqrt{a^2 + b^2} \)

Where:

\( A \): Area of the rectangle (mm², cm², m², in², or ft²);
\( P \): Perimeter of the rectangle (mm, cm, m, in, ft, or yd);
\( d \): Diagonal of the rectangle (mm, cm, m, in, ft, or yd);
\( a \): Length of the rectangle (mm, cm, m, in, ft, or yd);
\( b \): Width of the rectangle (mm, cm, m, in, ft, or yd).

Steps:

Enter the length (a) and width (b) of the rectangle along with their units (mm, cm, m, in, ft, or yd).
Convert all inputs to SI units (meters).
Calculate the area: \( A = a \times b \).
Calculate the perimeter: \( P = 2 \times (a + b) \).
Calculate the diagonal: \( d = \sqrt{a^2 + b^2} \).
Convert results to the selected output units (area in mm²/cm²/m²/in²/ft², perimeter and diagonal in mm/cm/m/in/ft/yd).
Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Rectangle Calculations

Calculating the properties of a rectangle is essential for:

Design and Architecture:

Engineering:

Education:

Everyday Applications:

4. Using the Calculator

Example 1 (Mixed Input Units): Calculate the properties of a rectangle:

Length: \( a = 5 \, \text{m} \);
Width: \( b = 300 \, \text{cm} \);
Area Output Unit: Square Meters (m²);
Perimeter Output Unit: Meters (m);
Diagonal Output Unit: Meters (m);
Convert width: \( b = 300 \times 0.01 = 3 \, \text{m} \);
Area: \( A = 5 \times 3 = 15 \, \text{m}^2 \);
Perimeter: \( P = 2 \times (5 + 3) = 16 \, \text{m} \);
Diagonal: \( d = \sqrt{5^2 + 3^2} = \sqrt{25 + 9} = \sqrt{34} \approx 5.8310 \, \text{m} \);
Result: \( A = 15.0000 \, \text{m}^2 \), \( P = 16.0000 \, \text{m} \), \( d = 5.8310 \, \text{m} \).

Example 2 (Mixed Output Units): Calculate the properties of a rectangle:

Length: \( a = 10 \, \text{yd} \);
Width: \( b = 18 \, \text{ft} \);
Area Output Unit: Square Feet (ft²);
Perimeter Output Unit: Yards (yd);
Diagonal Output Unit: Inches (in);
Convert to SI: \( a = 10 \times 0.9144 = 9.144 \, \text{m} \), \( b = 18 \times 0.3048 = 5.4864 \, \text{m} \);
Area: \( A = 9.144 \times 5.4864 \approx 50.1675 \, \text{m}^2 \approx 540.0000 \, \text{ft}^2 \);
Perimeter: \( P = 2 \times (9.144 + 5.4864) \approx 29.2608 \, \text{m} \approx 32.0000 \, \text{yd} \);
Diagonal: \( d = \sqrt{9.144^2 + 5.4864^2} \approx 10.6915 \, \text{m} \approx 420.9140 \, \text{in} \);
Result: \( A = 540.0000 \, \text{ft}^2 \), \( P = 32.0000 \, \text{yd} \), \( d = 420.9140 \, \text{in} \).

5. Frequently Asked Questions (FAQ)

Q: Can I use different units for each input and output?
A: Yes, the calculator allows independent unit selection for length, width, area, perimeter, and diagonal.

Q: What if I enter a negative value?
A: The calculator will display an error, as length and width must be positive.

Q: Why is the diagonal calculated?
A: The diagonal is useful for applications like bracing or determining the longest straight-line distance across the rectangle.