1. What is the Arccos (Inverse Cosine) Calculator?

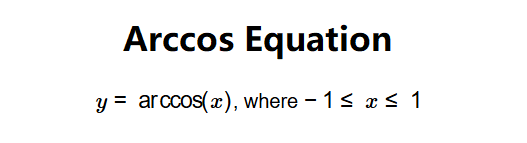
Definition: This calculator computes the inverse cosine (\( y = \arccos(x) \)) of a given value \( x \), where \( -1 \leq x \leq 1 \). The result is the angle \( y \) whose cosine is \( x \).

Purpose: It is used in mathematics, physics, and engineering to find angles based on cosine values, often in problems involving trigonometry, geometry, or wave analysis.

2. How Does the Calculator Work?

The calculator uses the inverse cosine function:

Where:

• \( x \): The input value (cosine of the angle)
• \( y \): The angle in radians or degrees

Unit Conversions:

• Angle (\( y \)):
  • Radians: The default output of the inverse cosine function
  • Degrees: Converted using \( \text{degrees} = \text{radians} \times \frac{180}{\pi} \)

Steps:

• Enter the value \( x \) (between -1 and 1).
• Click "Calculate" to compute \( y = \arccos(x) \).
• Select the desired unit (degrees or radians) for the result.
• The result is displayed with 4 decimal places.

3. Importance of Arccos Calculation

Calculating the inverse cosine is crucial for:

• Trigonometry: Finding angles in right triangles or other geometric shapes.
• Physics: Analyzing angles in wave mechanics, optics, or projectile motion.
• Engineering: Solving problems in signal processing, robotics, or structural analysis.

4. Using the Calculator

Example: Calculate the inverse cosine of \( x = 0.5 \).

1. Enter \( x = 0.5 \) in the input field.
2. Click "Calculate" to compute:
   • In radians: \( y = \arccos(0.5) = \frac{\pi}{3} \approx 1.0472 \, \text{radians} \)
   • In degrees: \( y = 1.0472 \times \frac{180}{\pi} = 60 \, \text{degrees} \)
3. Select the unit (degrees or radians) to view the result in the desired format.

5. Frequently Asked Questions (FAQ)

Q: What is the inverse cosine (arccos)?
A: The inverse cosine (\( \arccos(x) \)) is the angle \( y \) such that \( \cos(y) = x \), where \( -1 \leq x \leq 1 \). The result is typically between 0 and \( \pi \) radians (or 0° to 180°).

Q: Why must the input be between -1 and 1?
A: The cosine function only produces values between -1 and 1. Therefore, the inverse cosine is only defined for inputs in this range.

Q: What is the difference between radians and degrees?
A: Radians and degrees are two units for measuring angles. There are \( 2\pi \) radians in a full circle (360°), so 1 radian is approximately 57.2958 degrees, and 1 degree is approximately 0.01745 radians.

Arccos (Inverse Cosine) Calculator© - All Rights Reserved 2025