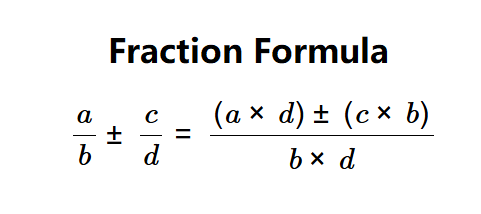Adding and Subtracting Fractions Calculator

First Fraction:

Operation:

Second Fraction:

1. What is the Adding and Subtracting Fractions Calculator?

Definition: This calculator performs addition or subtraction of two fractions and simplifies the result to its lowest terms.

Purpose: It assists students, educators, and anyone working with fractions to quickly compute the sum or difference of fractions without manual calculations, ensuring accuracy and simplicity.

2. How Does the Calculator Work?

The calculator uses the following formula for adding or subtracting fractions:

\[ \frac{a}{b} \pm \frac{c}{d} = \frac{(a \times d) \pm (c \times b)}{b \times d} \]

Where:

\( \frac{a}{b} \): First fraction (numerator \( a \), denominator \( b \));
\( \frac{c}{d} \): Second fraction (numerator \( c \), denominator \( d \));
\( \pm \): Addition or subtraction based on user selection.

Steps:

Enter the numerator and denominator of the first fraction.
Select the operation (add or subtract).
Enter the numerator and denominator of the second fraction.
Find a common denominator by calculating the least common multiple (LCM) of the denominators.
Convert both fractions to the common denominator.
Add or subtract the numerators as per the selected operation.
Simplify the resulting fraction by dividing the numerator and denominator by their greatest common divisor (GCD).
Display the simplified fraction and its decimal equivalent, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Adding and Subtracting Fractions

Performing fraction operations is crucial for:

Mathematics Education: Teaches fundamental concepts of fractions, which are essential for algebra, calculus, and beyond.
Everyday Calculations: Useful in cooking, budgeting, or DIY projects where measurements often involve fractions (e.g., adding \( \frac{1}{2} \) cup and \( \frac{1}{4} \) cup).
Engineering and Science: Fractions appear in ratios, proportions, and probability calculations.
Accuracy: Simplifying fractions ensures results are in their most understandable form.

4. Using the Calculator

Example 1 (Addition): Add two fractions:

First Fraction: \( \frac{3}{4} \);
Operation: Add;
Second Fraction: \( \frac{2}{3} \);
Common Denominator: \( 4 \times 3 = 12 \);
Adjust Fractions: \( \frac{3 \times 3}{4 \times 3} = \frac{9}{12} \), \( \frac{2 \times 4}{3 \times 4} = \frac{8}{12} \);
Add: \( \frac{9}{12} + \frac{8}{12} = \frac{17}{12} \);
Result: \( \frac{17}{12} \), Decimal: \( 1.4167 \).

Example 2 (Subtraction): Subtract two fractions:

First Fraction: \( \frac{5}{6} \);
Operation: Subtract;
Second Fraction: \( \frac{1}{4} \);
Common Denominator: \( 6 \times 4 = 24 \);
Adjust Fractions: \( \frac{5 \times 4}{6 \times 4} = \frac{20}{24} \), \( \frac{1 \times 6}{4 \times 6} = \frac{6}{24} \);
Subtract: \( \frac{20}{24} - \frac{6}{24} = \frac{14}{24} \);
Simplify: \( \frac{14 \div 2}{24 \div 2} = \frac{7}{12} \);
Result: \( \frac{7}{12} \), Decimal: \( 0.5833 \).

5. Frequently Asked Questions (FAQ)

Q: Why do we need a common denominator?
A: A common denominator allows the fractions to be combined by ensuring the units (denominators) are the same, making addition or subtraction of the numerators possible.

Q: What if the result is an improper fraction?
A: The calculator keeps the result as an improper fraction (e.g., \( \frac{17}{12} \)) and provides the decimal equivalent for clarity.

Q: Can this calculator handle negative fractions?
A: Yes, you can input negative numerators or denominators. The calculator adjusts the sign during simplification, ensuring the denominator is always positive.