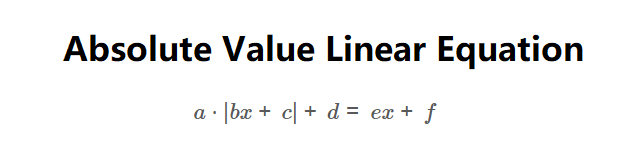1. What is an Absolute Value Linear Equation Calculator?

Definition: This calculator solves equations of the form \( a \cdot |bx + c| + d = ex + f \), where \( a, b, c, d, e, f \) are constants. The absolute value \( |bx + c| \) represents the distance of \( bx + c \) from zero, and the right-hand side is a linear expression.

Purpose: It assists in solving equations that model real-world scenarios involving distances or constraints, such as in physics, engineering, and optimization problems.

2. How Does the Calculator Work?

The calculator solves the equation \( a \cdot |bx + c| + d = ex + f \) using the following steps:

• Isolate the absolute value: \( |bx + c| = \frac{ex + f - d}{a} \)
• Case 1 (\( bx + c \geq 0 \)): \( bx + c = \frac{ex + f - d}{a} \)
• Solve: \( x = \frac{f - ac - d}{ab - e} \), then verify \( bx + c \geq 0 \).
• Case 2 (\( bx + c < 0 \)): \( -(bx + c) = \frac{ex + f - d}{a} \)
• Solve: \( x = \frac{-d + ac + f}{-ab - e} \), then verify \( bx + c < 0 \).

Where:

• \( a \): Multiplier of the absolute value expression;
• \( b \): Coefficient of \( x \) inside the absolute value;
• \( c \): Constant inside the absolute value;
• \( d \): Constant added outside the absolute value;
• \( e \): Coefficient of \( x \) on the right-hand side;
• \( f \): Constant on the right-hand side;
• Results are displayed with 4 decimal places or in scientific notation if less than 0.001.

Graphing Instructions

Step	Description
1	Plot \( y = a \cdot |bx + c| + d \), a V-shaped graph with vertex at \( x = -\frac{c}{b} \).
2	Plot \( y = ex + f \), a straight line through points \( (0, f) \) and \( (-f/e, 0) \) (if \( e \neq 0 \)).
3	Find intersections of the V-shape and the line; these are the solutions.

Notes:

• The V-shape opens up if \( a > 0 \), down if \( a < 0 \).
• The line’s slope is \( e \); if \( e = 0 \), it’s horizontal.
• Intersections may yield 0, 1, or 2 solutions.

Steps to Use:

• Enter coefficients \( a, b, c, d, e, f \).
• Click "Calculate" to compute solutions.
• View results, which may include zero, one, or two solutions.

3. Importance of Absolute Value Linear Equations

Solving such equations is crucial for:

• Modeling Constraints: Used in optimization to represent bounds or distances.
• Physics and Engineering: Models scenarios like motion with boundaries or error margins.
• Data Analysis: Helps in fitting models with absolute deviations.

4. Using the Calculator

Example 1: Solve \( 2 \cdot |x - 3| + 1 = x + 4 \):

• Inputs: \( a = 2, b = 1, c = -3, d = 1, e = 1, f = 4 \);
• Case 1 (\( x - 3 \geq 0 \)): \( x - 3 = \frac{x + 4 - 1}{2} \Rightarrow x = 7 \), and \( 7 - 3 = 4 \geq 0 \), valid;
• Case 2 (\( x - 3 < 0 \)): \( -(x - 3) = \frac{x + 4 - 1}{2} \Rightarrow x = 1 \), and \( 1 - 3 = -2 < 0 \), valid;
• Result: \( x = 7.0000, x = 1.0000 \).

Example 2: Solve \( |2x + 4| = 3x + 1 \):

• Inputs: \( a = 1, b = 2, c = 4, d = 0, e = 3, f = 1 \);
• Case 1 (\( 2x + 4 \geq 0 \)): \( 2x + 4 = \frac{3x + 1}{1} \Rightarrow x = 3 \), and \( 2(3) + 4 = 10 \geq 0 \), valid;
• Case 2 (\( 2x + 4 < 0 \)): \( -(2x + 4) = \frac{3x + 1}{1} \Rightarrow x = -1 \), and \( 2(-1) + 4 = 2 \geq 0 \), invalid;
• Result: \( x = 3.0000 \).

Example 3: Solve \( 2 \cdot |x + 1| + 2 = 5 \):

• Inputs: \( a = 2, b = 1, c = 1, d = 2, e = 0, f = 5 \);
• Case 1 (\( x + 1 \geq 0 \)): \( x + 1 = \frac{5 - 2}{2} \Rightarrow x = 0.5 \), and \( 0.5 + 1 = 1.5 \geq 0 \), valid;
• Case 2 (\( x + 1 < 0 \)): \( -(x + 1) = \frac{5 - 2}{2} \Rightarrow x = -2.5 \), and \( -2.5 + 1 = -1.5 < 0 \), valid;
• Result: \( x = 0.5000, x = -2.5000 \).

5. Frequently Asked Questions (FAQ)

Q: What does the absolute value represent?
A: The absolute value \( |bx + c| \) is the distance of \( bx + c \) from zero, always non-negative.

Q: Why might there be no solutions?
A: If the V-shaped graph and the line do not intersect, or if solutions don’t satisfy the absolute value condition, there are no solutions.

Q: Can this calculator handle non-linear right-hand sides?
A: No, this calculator is designed for a linear right-hand side (\( ex + f \)).

Absolute Value Linear Equation Calculator© - All Rights Reserved 2025