45-45-90 Triangle Calculator

Leg \( b \):

Hypotenuse \( c \):

Area:

Perimeter:

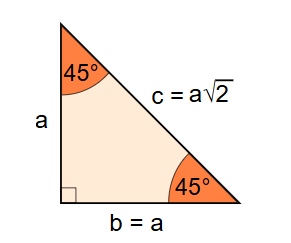
1. What is a 45-45-90 Triangle Calculator?

Definition: This calculator computes the sides, area, and perimeter of a 45-45-90 triangle given the length of one leg \( a \).

Purpose: It is used in geometry and engineering to determine the properties of a 45-45-90 triangle, which is an isosceles right triangle with fixed side ratios.

2. How Does the Calculator Work?

The calculator uses the following formulas for a 45-45-90 triangle, where \( a \) is one of the legs:

Leg \( b \): \( b = a \) (since the triangle is isosceles)
Hypotenuse \( c \): \( c = a \sqrt{2} \)
Area: \( \text{Area} = \frac{1}{2} a^2 \)
Perimeter: \( \text{Perimeter} = a + b + c = 2a + a\sqrt{2} \)

Unit Conversions:

Input Dimensions: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)
Output Sides and Perimeter: m, cm, mm, in, ft, yd
Output Area: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²)

Steps:

Input the length of leg \( a \) with its unit.
Convert the dimension to meters for calculation.
Calculate \( b \), \( c \), area, and perimeter using the formulas.
Convert each result to its respective selected unit for display, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of 45-45-90 Triangle Calculations

Calculating the properties of a 45-45-90 triangle is crucial for:

Geometry Education: Understanding special triangles and their properties.
Engineering Design: Using isosceles right triangles in structural components.
Trigonometry Applications: Simplifying calculations involving 45° angles.

4. Using the Calculator

Examples:

Example 1: For a triangle with \( a = 10 \, \text{cm} \):
- Convert: \( a = 10 / 100 = 0.1 \, \text{m} \)
- Leg \( b \): \( b = a = 0.1 \, \text{m} \)
- Hypotenuse \( c \): \( c = a \sqrt{2} = 0.1 \times \sqrt{2} = 0.1414 \, \text{m} \)
- Area: \( \text{Area} = \frac{1}{2} a^2 = \frac{1}{2} \times 0.1^2 = 0.005 \, \text{m}^2 \)
- Perimeter: \( \text{Perimeter} = 2a + a\sqrt{2} = 2 \times 0.1 + 0.1414 = 0.3414 \, \text{m} \)
- Convert: \( b = 10 \, \text{cm} \), \( c = 14.14 \, \text{cm} \), Area = \( 50 \, \text{cm}^2 \), Perimeter = \( 34.14 \, \text{cm} \)
Example 2: For a triangle with \( a = 2 \, \text{ft} \):
- Convert: \( a = 2 / 3.28084 = 0.6096 \, \text{m} \)
- Leg \( b \): \( b = a = 0.6096 \, \text{m} \)
- Hypotenuse \( c \): \( c = a \sqrt{2} = 0.6096 \times \sqrt{2} = 0.8622 \, \text{m} \)
- Area: \( \text{Area} = \frac{1}{2} a^2 = \frac{1}{2} \times 0.6096^2 = 0.1858 \, \text{m}^2 \)
- Perimeter: \( \text{Perimeter} = 2a + a\sqrt{2} = 2 \times 0.6096 + 0.8622 = 2.0814 \, \text{m} \)
- Convert: \( b = 2 \, \text{ft} \), \( c = 2.8284 \, \text{ft} \), Area = \( 2 \, \text{ft}^2 \), Perimeter = \( 6.8284 \, \text{ft} \)

5. Frequently Asked Questions (FAQ)

Q: What is a 45-45-90 triangle?
A: A 45-45-90 triangle is an isosceles right triangle with two 45° angles and one 90° angle, where the legs are equal, and the hypotenuse is \( \sqrt{2} \) times the leg length.

Q: Why are 45-45-90 triangles important?
A: They have consistent side ratios, making them useful in trigonometry, geometry, and engineering for simplifying calculations.