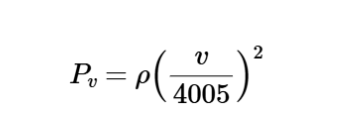Velocity Pressure for Air in Ducts Calculator

1. What is a Velocity Pressure Calculator?

Definition: This calculator computes the velocity pressure (\( P_v \)) in an air duct, representing the kinetic energy component of the total pressure, adjusted for air density.

Purpose: It is used in HVAC design to analyze air flow dynamics in ducts, aiding in the sizing of fans, ducts, and other ventilation components for efficient system performance.

2. How Does the Calculator Work?

The calculator uses the following formula for velocity pressure:

Velocity Pressure: \[ P_v = \rho \left( \frac{v}{4005} \right)^2 \]

Where:

\( P_v \): Velocity pressure (in. of water, Pa)
\( \rho \): Air density (lb_f/ft³, kg/m³)
\( v \): Average velocity (fpm, m/s)

Unit Conversions:

Air Density (\( \rho \)): lb_f/ft³, kg/m³ (1 kg/m³ = 0.062428 lb_f/ft³)
Velocity (\( v \)): fpm, m/s (1 m/s = 196.850 fpm)
Velocity Pressure (\( P_v \)): in. of water, Pa (1 in. of water = 248.84 Pa)

Steps:

Enter the air density (\( \rho \)) and average velocity (\( v \)), and select their units.
Convert \( \rho \) to lb_f/ft³ and \( v \) to fpm.
Calculate the velocity pressure using the formula, with the constant 4005 fpm.
Convert the result to the selected unit (in. of water or Pa).
Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Velocity Pressure Calculation

Calculating velocity pressure is crucial for:

HVAC System Design: Determines the dynamic pressure in ducts, aiding in fan selection and duct sizing.
Energy Efficiency: Optimizes air flow to minimize pressure losses, reducing energy consumption.
System Performance: Ensures adequate air distribution for ventilation and thermal comfort.

4. Using the Calculator

Examples:

Example 1: For \( \rho = 0.075 \, \text{lb_f/ft³} \), \( v = 2000 \, \text{fpm} \), velocity pressure in in. of water:
- \( P_v = 0.075 \times \left( \frac{2000}{4005} \right)^2 \approx 0.075 \times 0.249219 \approx 0.018691 \)
- Since 0.018691 < 10000 and > 0.00001, display with 5 decimal places: \( 0.01869 \)
Example 2: For \( \rho = 1.2 \, \text{kg/m³} \), \( v = 10 \, \text{m/s} \), velocity pressure in Pa:
- Convert: \( \rho = 1.2 \times 0.062428 \approx 0.074914 \, \text{lb_f/ft³} \)
- \( v = 10 \times 196.850 \approx 1968.50 \, \text{fpm} \)
- \( P_v = 0.074914 \times \left( \frac{1968.50}{4005} \right)^2 \approx 0.074914 \times 0.241462 \approx 0.018087 \, \text{in. of water} \)
- Convert to Pa: \( 0.018087 \times 248.84 \approx 4.49996 \)
- Since 4.49996 < 10000 and > 0.00001, display with 5 decimal places: \( 4.49996 \)
Example 3: For \( \rho = 0.08 \, \text{lb_f/ft³} \), \( v = 3000 \, \text{fpm} \), velocity pressure in in. of water:
- \( P_v = 0.08 \times \left( \frac{3000}{4005} \right)^2 \approx 0.08 \times 0.560625 \approx 0.04485 \)
- Since 0.04485 < 10000 and > 0.00001, display with 5 decimal places: \( 0.04485 \)

5. Frequently Asked Questions (FAQ)

Q: What does velocity pressure represent?
A: Velocity pressure (\( P_v \)) quantifies the kinetic energy of air flowing in a duct, contributing to the total pressure in HVAC systems.

Q: How can I determine air density?
A: Air density (\( \rho \)) can be calculated using the ideal gas law or obtained from standard tables (e.g., 0.075 lb_f/ft³ at 70°F and 1 atm), adjusted for temperature and pressure.

Q: Why is velocity pressure important in HVAC design?
A: It helps engineers design ducts and select fans to ensure efficient air flow, minimizing energy losses and maintaining system performance.