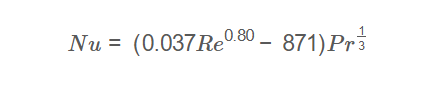
Turbulent Flow Over Flat Surface Calculator

1. What is a Turbulent Flow Over Flat Surface Calculator?

Definition: This calculator computes the average Nusselt number ( $N u$ ) for turbulent flow over a flat surface, accounting for the laminar-to-turbulent transition.

Purpose: It is used in HVAC systems to determine heat transfer coefficients ( $h$ ) for external air flows over walls or heat exchanger surfaces.

2. How Does the Calculator Work?

The calculator uses the following formula for turbulent flow over a flat surface:

Nusselt Number: $N u = (0.037 R e^{0.80} - 871) P r^{\frac{1}{3}}$

Where:

$N u$ : Nusselt number (dimensionless)
$R e$ : Reynolds number (dimensionless, based on surface length, user input)
$P r$ : Prandtl number (dimensionless, user input)

Steps:

Enter the Reynolds number ( $R e$ ) and Prandtl number ( $P r$ ).
Validate that $R e > 5 \times 10^{5}$ (turbulent flow requirement for this formula).
Calculate the Nusselt number using the given formula.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Turbulent Flow Over Flat Surface Calculation

Calculating the Nusselt number for turbulent flow over a flat surface is crucial for:

HVAC Design: Determines heat transfer coefficients for air flows over walls or heat exchanger surfaces, optimizing system performance.
Energy Efficiency: Helps design systems that efficiently transfer heat, reducing energy consumption.
System Performance: Ensures accurate thermal load calculations for heating and cooling systems.

4. Using the Calculator

Examples:

Example 1: For $R e = 600000$ , $P r = 0.7$ :
- Term 1: $0.037 \times (600000)^{0.80} - 871 \approx 0.037 \times 7944.15 - 871 \approx - 576.7655$
- Nusselt Number: $N u = - 576.7655 \times 0.8879 \approx - 512.1103$
- Error: Nusselt number must be positive. This indicates the formula may not be applicable for these inputs (check $R e$ and $P r$ ).
Example 2: For $R e = 1000000$ , $P r = 0.72$ :
- Term 1: $0.037 \times (1000000)^{0.80} - 871 \approx 0.037 \times 15848.931 - 871 \approx - 284.3895$
- Nusselt Number: $N u = - 284.3895 \times 0.896 \approx - 254.8129$
- Error: Nusselt number must be positive. This indicates the formula may not be applicable for these inputs (check $R e$ and $P r$ ).

Note: The examples above result in negative Nusselt numbers, which is not physically realistic. This suggests that the formula may require adjustment for certain ranges of $R e$ and $P r$ , or the provided formula may have a typo (e.g., the constant 871 may need adjustment, or additional terms may be required). In practice, Nusselt numbers should be positive. For typical turbulent flow over a flat plate with $R e > 5 \times 10^{5}$ , alternative correlations like $N u = 0.037 R e^{0.80} P r^{\frac{1}{3}}$ (without the -871 term) are often used. Please verify the formula with the source material (PAGE23 (1-13)) or use an adjusted version.

5. Frequently Asked Questions (FAQ)

Q: What is the turbulent flow over flat surface formula?
A: It calculates the average Nusselt number for turbulent flow over a flat surface as $N u = (0.037 R e^{0.80} - 871) P r^{\frac{1}{3}}$ , applicable for $R e > 5 \times 10^{5}$ .

Q: Why is this calculation important in HVAC systems?
A: It determines heat transfer coefficients for air flows over flat surfaces like walls or heat exchanger surfaces, optimizing HVAC system design.

Q: How do I determine the Reynolds number ( $R e$ ) and Prandtl number ( $P r$ )?
A: $R e$ can be calculated using a Reynolds Number Calculator with fluid properties and surface length, while $P r$ depends on fluid properties like viscosity, specific heat, and thermal conductivity, often available in engineering references.