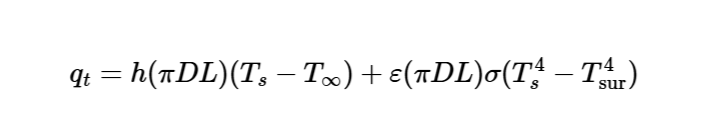Home Back

Total Heat Loss with Convection and Radiation Calculator

Total Heat Loss with Convection and Radiation

dimensionless (0 to 1)

1. What is a Total Heat Loss Calculator?

Definition: This calculator computes the total heat loss per unit length (\( q_t \)) from a cylindrical surface, combining convective heat transfer to the surrounding air and radiative exchange with the surroundings.

Purpose: It is used in thermal engineering and HVAC systems to quantify heat losses from pipes or cylindrical surfaces, aiding in insulation design and energy efficiency analysis.

2. How Does the Calculator Work?

The calculator uses the following formula for total heat loss:

Total Heat Loss: \[ q_t = h (\pi D L) (T_s - T_{\infty}) + \varepsilon (\pi D L) \sigma (T_s^4 - T_{\text{sur}}^4) \]

Where:

  • \( q_t \): Total heat loss per unit length (Btu/hr, W)
  • \( h \): Convection heat transfer coefficient (Btu/hr-ft²-°F, W/m²-K)
  • \( D \): Diameter of the pipe (ft, m)
  • \( L \): Length of the pipe (ft, m)
  • \( T_s \): Surface temperature (°F, °C, K, °R)
  • \( T_{\infty} \): Ambient air temperature (°F, °C, K, °R)
  • \( T_{\text{sur}} \): Surrounding surface temperature (°F, °C, K, °R)
  • \( \varepsilon \): Emissivity (dimensionless, 0 to 1)
  • \( \sigma \): Stefan-Boltzmann constant (\( 0.1714 \times 10^{-8} \text{ Btu/hr-ft²-°R}^4 \))

Unit Conversions:

  • Convection Coefficient (\( h \)): Btu/hr-ft²-°F, W/m²-K (1 W/m²-K = 0.176110 Btu/hr-ft²-°F)
  • Diameter (\( D \)) and Length (\( L \)): ft, m (1 m = 3.28084 ft)
  • Temperatures (\( T_s \), \( T_{\infty} \), \( T_{\text{sur}} \)):
    • °F to °F: No conversion (for convection)
    • °C to °F: °F = (°C × 9/5) + 32 (for convection)
    • K to °F: °F = ((K - 273.15) × 9/5) + 32 (for convection)
    • °R to °F: °F = °R - 460 (for convection)
    • °F to °R: °R = °F + 460 (for radiation)
    • °C to °R: °F = (°C × 9/5) + 32, then °R = °F + 460 (for radiation)
    • K to °R: °C = K - 273.15, then °F = (°C × 9/5) + 32, then °R = °F + 460 (for radiation)
    • °R to °R: No conversion (for radiation)
  • Total Heat Loss (\( q_t \)): Btu/hr, W (1 Btu/hr = 0.293071 W)

Steps:

  • Enter the convection coefficient (\( h \)), pipe diameter (\( D \)), pipe length (\( L \)), surface temperature (\( T_s \)), ambient air temperature (\( T_{\infty} \)), surrounding surface temperature (\( T_{\text{sur}} \)), and emissivity (\( \varepsilon \)), and select their units.
  • Convert \( h \), \( D \), and \( L \) to Btu/hr-ft²-°F, ft, and ft, respectively.
  • Convert \( T_s \) and \( T_{\infty} \) to °F for convection; convert \( T_s \) and \( T_{\text{sur}} \) to °R for radiation.
  • Calculate convection heat loss: \( h (\pi D L) (T_s - T_{\infty}) \).
  • Calculate radiation heat loss: \( \varepsilon (\pi D L) \sigma (T_s^4 - T_{\text{sur}}^4) \).
  • Sum the two components to get \( q_t \).
  • Convert the result to the selected unit (Btu/hr or W).
  • Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Total Heat Loss Calculation

Calculating total heat loss is crucial for:

  • HVAC and Piping Design: Quantifies heat losses from pipes, aiding in insulation selection and system sizing.
  • Energy Efficiency: Helps minimize energy losses by optimizing insulation and surface properties.
  • Thermal Management: Ensures proper temperature control in industrial processes involving heated pipes.

4. Using the Calculator

Examples:

  • Example 1: For \( h = 3 \, \text{Btu/hr-ft²-°F} \), \( D = 0.25 \, \text{ft} \), \( L = 1 \, \text{ft} \), \( T_s = 860 \, \text{°R} \), \( T_{\infty} = 75 \, \text{°F} \), \( T_{\text{sur}} = 535 \, \text{°R} \), \( \varepsilon = 0.80 \), heat loss in Btu/hr:
    • Convection: \( T_s = 860 - 460 = 400 \, \text{°F} \), \( q_{\text{conv}} = 3 \times \pi \times 0.25 \times 1 \times (400 - 75) \approx 765.765 \)
    • Radiation: \( q_{\text{rad}} = 0.80 \times \pi \times 0.25 \times 1 \times 0.1714 \times 10^{-8} \times (860^4 - 535^4) \approx 511.984 \)
    • Total: \( q_t = 765.765 + 511.984 \approx 1277.749 \)
    • Since 1277.749 < 10000 and > 0.00001, display with 5 decimal places: \( 1277.74900 \)
  • Example 2: For \( h = 17 \, \text{W/m²-K} \), \( D = 0.0762 \, \text{m} \), \( L = 0.3048 \, \text{m} \), \( T_s = 200 \, \text{°C} \), \( T_{\infty} = 298.15 \, \text{K} \), \( T_{\text{sur}} = 25 \, \text{°C} \), \( \varepsilon = 0.90 \), heat loss in W:
    • Convert: \( h = 17 \times 0.176110 = 2.99387 \, \text{Btu/hr-ft²-°F} \), \( D = 0.0762 \times 3.28084 = 0.25 \, \text{ft} \), \( L = 0.3048 \times 3.28084 = 1 \, \text{ft} \)
    • Convection: \( T_s = (200 \times 9/5) + 32 = 392 \, \text{°F} \), \( T_{\infty} = (298.15 - 273.15) = 25 \, \text{°C} \), \( T_{\infty} = (25 \times 9/5) + 32 = 77 \, \text{°F} \)
    • \( q_{\text{conv}} = 2.99387 \times \pi \times 0.25 \times 1 \times (392 - 77) \approx 739.638 \)
    • Radiation: \( T_s = (200 \times 9/5) + 32 + 460 = 852 \, \text{°R} \), \( T_{\text{sur}} = (25 \times 9/5) + 32 + 460 = 537 \, \text{°R} \)
    • \( q_{\text{rad}} = 0.90 \times \pi \times 0.25 \times 1 \times 0.1714 \times 10^{-8} \times (852^4 - 537^4) \approx 505.009 \)
    • Total: \( q_t = 739.638 + 505.009 \approx 1244.647 \, \text{Btu/hr} \)
    • Convert to W: \( 1244.647 \times 0.293071 \approx 364.723 \)
    • Since 364.723 < 10000 and > 0.00001, display with 5 decimal places: \( 364.72300 \)
  • Example 3: For \( h = 5 \, \text{Btu/hr-ft²-°F} \), \( D = 0.5 \, \text{ft} \), \( L = 1 \, \text{ft} \), \( T_s = 473.15 \, \text{K} \), \( T_{\infty} = 293.15 \, \text{K} \), \( T_{\text{sur}} = 530 \, \text{°R} \), \( \varepsilon = 0.70 \), heat loss in Btu/hr:
    • Convert: \( T_s = (473.15 - 273.15) = 200 \, \text{°C} \), \( T_s = (200 \times 9/5) + 32 = 392 \, \text{°F} \), \( T_s_R = 392 + 460 = 852 \, \text{°R} \)
    • \( T_{\infty} = (293.15 - 273.15) = 20 \, \text{°C} \), \( T_{\infty} = (20 \times 9/5) + 32 = 68 \, \text{°F} \)
    • Radiation: \( T_{\text{sur}} = 530 \, \text{°R} \)
    • Convection: \( q_{\text{conv}} = 5 \times \pi \times 0.5 \times 1 \times (392 - 68) \approx 2546.900 \)
    • Radiation: \( q_{\text{rad}} = 0.70 \times \pi \times 0.5 \times 1 \times 0.1714 \times 10^{-8} \times (852^4 - 530^4) \approx 871.796 \)
    • Total: \( q_t = 2546.900 + 871.796 \approx 3418.696 \)
    • Since 3418.696 < 10000 and > 0.00001, display with 5 decimal places: \( 3418.69600 \)

5. Frequently Asked Questions (FAQ)

Q: What does total heat loss per unit length represent?
A: Total heat loss per unit length (\( q_t \)) quantifies the combined convective and radiative heat transfer from a cylindrical surface, such as a pipe, per unit length.

Q: Why is this calculation important for piping systems?
A: It helps engineers determine heat losses from pipes, enabling the design of appropriate insulation to minimize energy losses and maintain process temperatures.

Q: How can I determine the convection coefficient or emissivity?
A: The convection coefficient (\( h \)) can be calculated using empirical correlations or measured experimentally. Emissivity (\( \varepsilon \)) is obtained from material property tables or manufacturer specifications.

Total Heat Loss with Convection and Radiation Calculator© - All Rights Reserved 2025