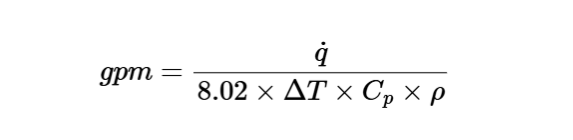Home Back

Temperature drop to GPM Calculator

Temperature drop to GPM Calculator

1. What is a Flow Rate Through Convector or Terminal Unit Calculator?

Definition: This calculator computes the water flow rate (\( gpm \)) through a convector or terminal unit in a hydronic system, based on heat capacity, temperature drop, specific heat, and water density.

Purpose: It is used in hydronic heating and cooling system design to determine the required water flow rate, aiding in system sizing, pump selection, and energy efficiency.

2. How Does the Calculator Work?

The calculator uses the following formula for water flow rate:

Water Flow Rate: \[ gpm = \frac{\dot{q}}{8.02 \times \Delta T \times C_p \times \rho} \]

Where:

  • \( gpm \): Water flow rate (gallon/min, m³/s)
  • \( \dot{q} \): Heat capacity of the terminal unit (Btu/hr, W)
  • \( \Delta T \): Temperature drop across the convector or terminal unit (°F, °C)
  • \( C_p \): Specific heat of water (Btu/lb·°F, kJ/kg·K)
  • \( \rho \): Density of water (lb/ft³, kg/m³)

Unit Conversions:

  • Heat Capacity (\( \dot{q} \)): Btu/hr, W (1 W = 3.41214 Btu/hr)
  • Temperature Drop (\( \Delta T \)): °F, °C (1 °C = 1.8 °F)
  • Specific Heat (\( C_p \)): Btu/lb·°F, kJ/kg·K (1 kJ/kg·K = 0.2388459 Btu/lb·°F)
  • Water Density (\( \rho \)): lb/ft³, kg/m³ (1 kg/m³ = 0.062428 lb/ft³)
  • Flow Rate (\( gpm \)): gpm, m³/s (1 gpm = 6.30902e-5 m³/s)

Steps:

  • Enter the heat capacity (\( \dot{q} \)), temperature drop (\( \Delta T \)), specific heat (\( C_p \)), and water density (\( \rho \)), and select their units.
  • Convert \( \dot{q} \), \( \Delta T \), \( C_p \), and \( \rho \) to Btu/hr, °F, Btu/lb·°F, and lb/ft³, respectively.
  • Calculate the flow rate using the formula.
  • Convert the result to the selected unit (gpm or m³/s).
  • Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Flow Rate Calculation

Calculating the water flow rate through a convector or terminal unit is crucial for:

  • Hydronic System Design: Ensures proper water flow to meet heating or cooling demands, optimizing system performance.
  • Energy Efficiency: Balances flow rates to minimize pump energy consumption.
  • Equipment Selection: Guides the selection of pumps, pipes, and terminal units for efficient operation.

4. Using the Calculator

Examples:

  • Example 1: For \( \dot{q} = 10000 \, \text{Btu/hr} \), \( \Delta T = 20 \, \text{°F} \), \( C_p = 1 \, \text{Btu/lb·°F} \), \( \rho = 62.4 \, \text{lb/ft³} \), flow rate in gpm:
    • \( gpm = \frac{10000}{8.02 \times 20 \times 1 \times 62.4} \approx \frac{10000}{10001.856} \approx 1 \)
    • Since 1 < 10000 and > 0.00001, display with 5 decimal places: \( 1.00000 \)
  • Example 2: For \( \dot{q} = 2930.7 \, \text{W} \), \( \Delta T = 11.11 \, \text{°C} \), \( C_p = 4.18 \, \text{kJ/kg·K} \), \( \rho = 1000 \, \text{kg/m³} \), flow rate in m³/s:
    • Convert: \( \dot{q} = 2930.7 \times 3.41214 \approx 10000 \, \text{Btu/hr} \)
    • \( \Delta T = 11.11 \times 1.8 \approx 20 \, \text{°F} \)
    • \( C_p = 4.18 \times 0.2388459 \approx 0.998375 \, \text{Btu/lb·°F} \)
    • \( \rho = 1000 \times 0.062428 \approx 62.428 \, \text{lb/ft³} \)
    • \( gpm = \frac{10000}{8.02 \times 20 \times 0.998375 \times 62.428} \approx \frac{10000}{9998.34} \approx 1.00017 \)
    • Convert to m³/s: \( 1.00017 \times 6.30902e-5 \approx 6.3096e-5 \)
    • Since 6.3096e-5 < 0.00001, display in scientific notation: \( 6.30960 \times 10^{-5} \)
  • Example 3: For \( \dot{q} = 15000 \, \text{Btu/hr} \), \( \Delta T = 15 \, \text{°F} \), \( C_p = 1 \, \text{Btu/lb·°F} \), \( \rho = 60 \, \text{lb/ft³} \), flow rate in gpm:
    • \( gpm = \frac{15000}{8.02 \times 15 \times 1 \times 60} \approx \frac{15000}{7214.4} \approx 2.0786 \)
    • Since 2.0786 < 10000 and > 0.00001, display with 5 decimal places: \( 2.07860 \)

5. Frequently Asked Questions (FAQ)

Q: What does flow rate through a convector or terminal unit represent?
A: The flow rate (\( gpm \)) quantifies the volume of water per unit time required to transfer heat through a convector or terminal unit in a hydronic system, critical for system performance.

Q: How can I determine the input parameters?
A: Heat capacity (\( \dot{q} \)) is determined from the heating or cooling load of the terminal unit. Temperature drop (\( \Delta T \)) is designed or measured across the unit. Specific heat (\( C_p \)) is typically 1 Btu/lb·°F or 4.18 kJ/kg·K for water. Water density (\( \rho \)) is typically 62.4 lb/ft³ or 1000 kg/m³, adjusted for temperature.

Q: Why is flow rate important in hydronic system design?
A: It ensures adequate water flow to meet heating or cooling demands, optimizing energy efficiency and system performance while guiding equipment selection.

Flow Rate Through Convector or Terminal Unit Calculator© - All Rights Reserved 2025