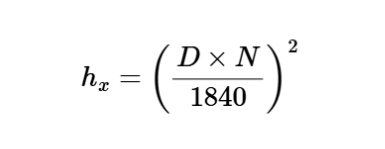Shut-Off Head Calculator

Shut-Off Head Calculator - Maximum (Shut-Off) Head of a Centrifugal Pump

1. What is a Maximum (Shut-Off) Head Calculator?

Definition: This calculator computes the maximum head (\( h_x \)), or shut-off head, developed by a centrifugal pump when the discharge valve is closed, based on the impeller diameter (\( D \)) and rotation speed (\( N \)).

Purpose: It is used in pump system design to determine the maximum head a centrifugal pump can generate, aiding in pump selection, system safety, and performance optimization.

2. How Does the Calculator Work?

The calculator uses the following formula for shut-off head:

Shut-Off Head: \[ h_x = \left( \frac{D \times N}{1840} \right)^2 \]

Where:

\( h_x \): Shut-off head (ft, m)
\( D \): Outside diameter of the impeller (in., m)
\( N \): Speed of rotation (rpm)

Unit Conversions:

Impeller Diameter (\( D \)): in., m (1 m = 39.3701 in.)
Shut-Off Head (\( h_x \)): ft, m (1 ft = 0.3048 m)

Steps:

Enter the impeller diameter (\( D \)) and rotation speed (\( N \)), and select the diameter unit.
Convert \( D \) to in.
Calculate the shut-off head using the formula with the constant 1840.
Convert the result to the selected unit (ft or m).
Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Shut-Off Head Calculation

Calculating the shut-off head is crucial for:

Pump System Design: Ensures the pump's maximum head is known to prevent overpressure when the discharge valve is closed.
System Safety: Protects system components by accounting for the highest possible head the pump can generate.
Pump Selection: Guides the selection of pumps that match system requirements, optimizing performance and reliability.

4. Using the Calculator

Examples:

Example 1: For \( D = 9.5 \, \text{in.} \), \( N = 1750 \, \text{rpm} \), head in ft:
- \( h_x = \left( \frac{9.5 \times 1750}{1840} \right)^2 \approx \left( \frac{16625}{1840} \right)^2 \approx (9.03533)^2 \approx 81.637 \)
- Since 81.637 < 10000 and > 0.00001, display with 5 decimal places: \( 81.63700 \)
- Note: The calculated value (81.637 ft) is very close to the example output of 81.5 ft, with minor differences due to rounding.
Example 2: For \( D = 0.2413 \, \text{m} \), \( N = 1750 \, \text{rpm} \), head in m:
- Convert: \( D = 0.2413 \times 39.3701 \approx 9.5 \, \text{in.} \)
- \( h_x = \left( \frac{9.5 \times 1750}{1840} \right)^2 \approx 81.637 \, \text{ft} \)
- Convert to m: \( 81.637 \times 0.3048 \approx 24.883 \)
- Since 24.883 < 10000 and > 0.00001, display with 5 decimal places: \( 24.88300 \)
Example 3: For \( D = 12 \, \text{in.} \), \( N = 1500 \, \text{rpm} \), head in ft:
- \( h_x = \left( \frac{12 \times 1500}{1840} \right)^2 \approx \left( \frac{18000}{1840} \right)^2 \approx (9.78261)^2 \approx 95.699 \)
- Since 95.699 < 10000 and > 0.00001, display with 5 decimal places: \( 95.69900 \)

5. Frequently Asked Questions (FAQ)

Q: What does shut-off head represent?
A: Shut-off head (\( h_x \)) is the maximum head a centrifugal pump can develop when the discharge valve is closed, representing the pump's highest possible pressure output.

Q: How can I determine the input parameters?
A: Impeller diameter (\( D \)) is obtained from the pump's specifications (e.g., 9.5 in.). Rotation speed (\( N \)) is the pump's operating speed in rpm (e.g., 1750 rpm).

Q: Why is shut-off head important in pump system design?
A: It ensures the system is designed to handle the maximum head a pump can generate, preventing overpressure, ensuring safety, and guiding pump selection.