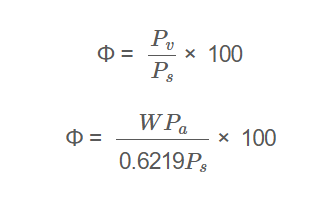Relative Humidity Calculator for HVAC Systems

Relative Humidity Calculator

Calculation Method:

Do you have \( P_s \) ?

Temperature (\( T \)) to Calculate \( P_s \):

Saturation Pressure (\( P_s \)):

Partial Pressure of Water Vapor (\( P_v \)):

Humidity Ratio (\( W \)):

Partial Pressure of Dry Air (\( P_a \)):

1. What is a Relative Humidity Calculator?

Definition: This calculator computes the relative humidity (\( \Phi \)), the ratio of the partial pressure of water vapor to the saturation pressure, or using the humidity ratio and partial pressure of dry air, expressed as a percentage.

Purpose: It is used in HVAC systems to quantify the moisture content in air relative to its maximum capacity at a given temperature, aiding in the design of air conditioning and ventilation systems.

2. How Does the Calculator Work?

The calculator provides two methods to calculate relative humidity:

Method 1 (Using \( P_v \) and \( P_s \)): \[ \Phi = \frac{P_v}{P_s} \times 100 \]

Method 2 (Using \( W \), \( P_a \), and \( P_s \)): \[ \Phi = \frac{W P_a}{0.6219 P_s} \times 100 \]

Saturation Pressure (\( P_s \)) Calculation (if not provided): \[ P_s = 0.61078 \exp\left(\frac{17.27 T}{T + 237.3}\right) \, \text{(kPa, where \( T \) is in °C)} \] Converted to psia for calculation.

Where:

\( \Phi \): Relative humidity (%)
\( P_v \): Partial pressure of water vapor (psia, inHg, Pa)
\( P_s \): Saturation pressure at temperature \( T \) (psia, inHg, Pa)
\( W \): Humidity ratio (lb_v/lb_da or kg_v/kg_da)
\( P_a \): Partial pressure of dry air (psia, inHg, Pa)
\( T \): Temperature (°F, °C, K)
Constant 0.6219: Ratio of molecular weights of water vapor to dry air (18.015/28.965)

Unit Conversions:

Pressures (\( P_v \), \( P_s \), \( P_a \)): psia, inHg (1 inHg = 0.491154 psia), Pa (1 Pa = 0.000145038 psia)
Temperature (\( T \)): °F, °C, K (°C = K - 273.15)
Humidity Ratio (\( W \)): lb_v/lb_da, kg_v/kg_da (numerically the same, label changes for clarity)

Steps:

Select the calculation method (Method 1 or Method 2).
Indicate whether you have \( P_s \) from Table 2-3 or need to calculate it from temperature.
Enter the required inputs based on the method:
- Method 1: Partial pressure of water vapor (\( P_v \)).
- Method 2: Humidity ratio (\( W \)) and partial pressure of dry air (\( P_a \)).
If calculating \( P_s \), enter the temperature (\( T \)) and select its unit; otherwise, input \( P_s \) directly.
Convert all pressures to psia and temperature to °C (if calculating \( P_s \)).
Calculate the relative humidity using the selected method.
Display the result as a percentage, with 2 decimal places.

3. Importance of Relative Humidity Calculation

Calculating relative humidity is crucial for:

HVAC Design: Quantifies the moisture content in air relative to its maximum capacity, aiding in the design of air conditioning, dehumidification, and ventilation systems.
Comfort and Health: Ensures appropriate humidity levels for occupant comfort and indoor air quality.
System Performance: Enables accurate psychrometric calculations for HVAC system efficiency.

4. Using the Calculator

Examples:

Example 1 (Method 1): For \( P_v = 0.2036 \, \text{psia} \), \( P_s = 0.36328 \, \text{psia} \):
- \( \Phi = \frac{0.2036}{0.36328} \times 100 \approx 56.04\% \)
Example 2 (Method 2): For \( W = 0.008738 \), \( P_a = 14.4924 \, \text{psia} \), \( P_s = 0.36328 \, \text{psia} \):
- \( \Phi = \frac{0.008738 \times 14.4924}{0.6219 \times 0.36328} \times 100 \approx \frac{0.12662}{0.22584} \times 100 \approx 56.04\% \)
Example 3 (Method 1 with Calculated \( P_s \)): For \( T = 20 \, \text{°C} \), \( P_v = 1500 \, \text{Pa} \):
- Convert: \( P_v = 1500 \times 0.000145038 = 0.217557 \, \text{psia} \)
- Calculate \( P_s \): \( P_s = 0.61078 \times \exp\left(\frac{17.27 \times 20}{20 + 237.3}\right) \approx 0.61078 \times \exp(1.3408) \approx 2.3376 \, \text{kPa} \), \( P_s = 2.3376 \times 0.145038 \approx 0.3391 \, \text{psia} \)
- \( \Phi = \frac{0.217557}{0.3391} \times 100 \approx 64.15\% \)

5. Frequently Asked Questions (FAQ)

Q: What is relative humidity?
A: Relative humidity (\( \Phi \)) is the ratio of the partial pressure of water vapor (\( P_v \)) to the saturation pressure (\( P_s \)) at a given temperature, expressed as a percentage.

Q: Why is relative humidity important in HVAC systems?
A: It quantifies the moisture content in air relative to its maximum capacity, which is essential for designing systems that control humidity for comfort, health, and equipment performance.

Q: How do I determine the saturation pressure (\( P_s \)) if I don’t have Table 2-3?
A: The calculator uses the Magnus-Tetens formula to estimate \( P_s \) based on temperature, or you can provide \( P_s \) directly if known from external sources like psychrometric tables.