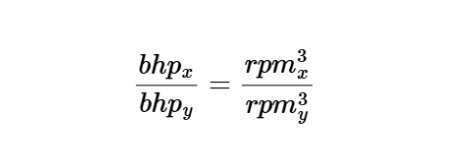Pump Laws Horsepower Calculator

1. What is a Pump Laws Horsepower Calculator?

Definition: This calculator predicts the change in brake horsepower (\( bhp_x \)) required by a centrifugal pump when its rotation speed changes from a known speed (\( rpm_y \)) to a new speed (\( rpm_x \)), with constant impeller diameter, based on the pump laws.

Purpose: It is used in pump system design to estimate how changes in pump speed affect power requirements, aiding in motor selection, energy efficiency, and system performance optimization.

2. How Does the Calculator Work?

The calculator uses the following formula for brake horsepower:

Brake Horsepower: \[ \frac{bhp_x}{bhp_y} = \frac{rpm_x^3}{rpm_y^3} \] or \[ bhp_x = bhp_y \times \frac{rpm_x^3}{rpm_y^3} \]

Where:

\( bhp_x \): New brake horsepower (hp, kW)
\( bhp_y \): Known brake horsepower (hp, kW)
\( rpm_x \): New rotation speed (rpm)
\( rpm_y \): Known rotation speed (rpm)

Unit Conversions:

Brake Horsepower (\( bhp_x \), \( bhp_y \)): hp, kW (1 kW = 1.34102 hp; 1 hp = 0.7457 kW)

Steps:

Enter the known brake horsepower (\( bhp_y \)), known rotation speed (\( rpm_y \)), and new rotation speed (\( rpm_x \)), and select the horsepower unit.
Convert \( bhp_y \) to hp.
Calculate the new brake horsepower using the formula.
Convert the result to the selected unit (hp or kW).
Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Pump Laws Horsepower Calculation

Calculating the change in brake horsepower due to speed changes is crucial for:

Pump System Design: Ensures the motor can provide sufficient power for the pump at different speeds, preventing overload or underperformance.
Energy Efficiency: Optimizes motor selection and speed adjustments to match power needs, reducing energy consumption.
System Reliability: Supports consistent pump performance by ensuring adequate power for varying operating conditions.

4. Using the Calculator

Examples:

Example 1: For \( bhp_y = 8.15 \, \text{hp} \), \( rpm_y = 1150 \, \text{rpm} \), \( rpm_x = 1750 \, \text{rpm} \), new brake horsepower in hp:
- \( bhp_x = 8.15 \times \frac{1750^3}{1150^3} \approx 8.15 \times \frac{5359375000}{1515737500} \approx 8.15 \times 3.52576 \approx 28.735 \)
- Since 28.735 < 10000 and > 0.00001, display with 5 decimal places: \( 28.73500 \)
- Note: The calculated value (28.735 hp) is close to the example output of 28.7 hp, with minor differences likely due to rounding in the original example.
Example 2: For \( bhp_y = 6.075 \, \text{kW} \), \( rpm_y = 1150 \, \text{rpm} \), \( rpm_x = 1750 \, \text{rpm} \), new brake horsepower in kW:
- Convert: \( bhp_y = 6.075 \times 1.34102 \approx 8.15 \, \text{hp} \)
- \( bhp_x = 8.15 \times \frac{1750^3}{1150^3} \approx 28.735 \, \text{hp} \)
- Convert to kW: \( 28.735 \times 0.7457 \approx 21.428 \)
- Since 21.428 < 10000 and > 0.00001, display with 5 decimal places: \( 21.42800 \)
Example 3: For \( bhp_y = 10 \, \text{hp} \), \( rpm_y = 1200 \, \text{rpm} \), \( rpm_x = 1500 \, \text{rpm} \), new brake horsepower in hp:
- \( bhp_x = 10 \times \frac{1500^3}{1200^3} \approx 10 \times \frac{3375000000}{1728000000} \approx 10 \times 1.953125 \approx 19.53125 \)
- Since 19.53125 < 10000 and > 0.00001, display with 5 decimal places: \( 19.53125 \)

5. Frequently Asked Questions (FAQ)

Q: What does the pump laws horsepower calculation represent?
A: The pump laws horsepower calculation predicts the new brake horsepower (\( bhp_x \)) required by a centrifugal pump when its rotation speed changes, assuming a constant impeller diameter, based on the cubic relationship between horsepower and speed.

Q: How can I determine the input parameters?
A: Known brake horsepower (\( bhp_y \)) is the current pump power requirement (e.g., 8.15 hp). Known rotation speed (\( rpm_y \)) is the current pump speed (e.g., 1150 rpm). New rotation speed (\( rpm_x \)) is the desired or adjusted pump speed (e.g., 1750 rpm).

Q: Why is the pump laws horsepower calculation important in pump system design?
A: It allows engineers to predict and adjust power requirements for varying operating conditions, ensuring efficient motor sizing, preventing overload, and supporting reliable system operation.