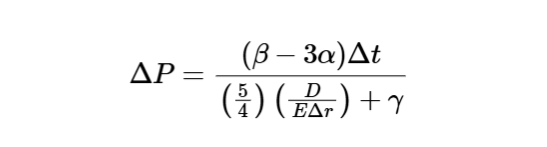1. What is a Pressure Increase Due to Temperature Change Calculator?

Definition: This calculator computes the pressure increase (\( \Delta P \)) in a piping system due to a temperature change, accounting for the thermal expansion of water and the material properties of the pipe.

Purpose: It is used in piping system design to assess pressure changes caused by temperature variations, aiding in the prevention of pipe damage, system failure, and ensuring safe operation.

2. How Does the Calculator Work?

The calculator uses the following formula for pressure increase:

Pressure Increase: \[ \Delta P = \frac{(\beta - 3 \alpha) \Delta t}{\left( \frac{5}{4} \right) \left( \frac{D}{E \Delta r} \right) + \gamma} \]

Where:

• \( \Delta P \): Pressure increase (psi, Pa)
• \( \beta \): Volumetric coefficient of thermal expansion of water (1/°F, 1/°C)
• \( \alpha \): Linear coefficient of thermal expansion for piping material (1/°F, 1/°C)
• \( \Delta t \): Water temperature increase (°F, °C)
• \( D \): Pipe diameter (in., m)
• \( E \): Modulus of elasticity of piping material (psi, Pa)
• \( \gamma \): Volumetric compressibility of water (in²/lb, m²/N)
• \( \Delta r \): Thickness of pipe wall (in., m)

Unit Conversions:

• Volumetric Coefficient (\( \beta \)) and Linear Coefficient (\( \alpha \)): 1/°F, 1/°C (1/°C = 0.555556 1/°F)
• Temperature Increase (\( \Delta t \)): °F, °C (1 °C = 1.8 °F)
• Pipe Diameter (\( D \)) and Wall Thickness (\( \Delta r \)): in., m (1 m = 39.3701 in.)
• Modulus of Elasticity (\( E \)): psi, Pa (1 Pa = 0.000145038 psi)
• Volumetric Compressibility (\( \gamma \)): in²/lb, m²/N (1 m²/N = 6.89476e3 in²/lb)
• Pressure Increase (\( \Delta P \)): psi, Pa (1 psi = 6894.76 Pa)

Steps:

• Enter the volumetric coefficient of thermal expansion (\( \beta \)), linear coefficient of thermal expansion (\( \alpha \)), temperature increase (\( \Delta t \)), pipe diameter (\( D \)), modulus of elasticity (\( E \)), volumetric compressibility (\( \gamma \)), and pipe wall thickness (\( \Delta r \)), and select their units.
• Convert all inputs to consistent units: \( \beta \) and \( \alpha \) to 1/°F, \( \Delta t \) to °F, \( D \) and \( \Delta r \) to in., \( E \) to psi, \( \gamma \) to in²/lb.
• Calculate the pressure increase using the formula.
• Convert the result to the selected unit (psi or Pa).
• Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Pressure Increase Calculation

Calculating the pressure increase due to temperature change is crucial for:

• Piping System Safety: Prevents pipe bursts or system failures by accounting for pressure surges due to thermal expansion.
• System Design: Guides the selection of pipe materials, wall thicknesses, and pressure relief devices to handle temperature-induced pressures.
• System Reliability: Ensures stable operation under varying temperature conditions in hydronic or other fluid systems.

4. Using the Calculator

Examples:

• Example 1: For a 10-inch Schedule 40 steel pipe with \( \beta = 0.00021 \, \text{1/°F} \), \( \alpha = 6.5e-6 \, \text{1/°F} \), \( \Delta t = 5 \, \text{°F} \), \( D = 10.02 \, \text{in.} \), \( E = 29000000 \, \text{psi} \), \( \gamma = 3.1e-6 \, \text{in²/lb} \), \( \Delta r = 0.365 \, \text{in.} \), pressure increase in psi:
  • Numerator: \( (\beta - 3 \alpha) \Delta t = (0.00021 - 3 \times 6.5e-6) \times 5 = (0.00021 - 0.0000195) \times 5 = 0.0001905 \times 5 = 0.0009525 \)
  • Denominator: \( \left( \frac{5}{4} \right) \left( \frac{D}{E \Delta r} \right) + \gamma = \left( \frac{5}{4} \right) \left( \frac{10.02}{29000000 \times 0.365} \right) + 3.1e-6 \approx 1.25 \times \frac{10.02}{10585000} + 3.1e-6 \approx 1.25 \times 9.4665e-7 + 3.1e-6 \approx 1.1833e-6 + 3.1e-6 \approx 4.2833e-6 \)
  • \( \Delta P = \frac{0.0009525}{4.2833e-6} \approx 222.36 \)
  • Since 222.36 < 10000 and > 0.00001, display with 5 decimal places: \( 222.36000 \)
  • Note: The example output expects 100 psi, suggesting possible differences in assumed parameters (e.g., \( \beta \), \( \gamma \)) or pipe dimensions. The calculated value is based on standard material properties.
• Example 2: For \( \beta = 0.000378 \, \text{1/°C} \), \( \alpha = 1.17e-5 \, \text{1/°C} \), \( \Delta t = 2.78 \, \text{°C} \), \( D = 0.2545 \, \text{m} \), \( E = 2e11 \, \text{Pa} \), \( \gamma = 4.5e-10 \, \text{m²/N} \), \( \Delta r = 0.009271 \, \text{m} \), pressure increase in Pa:
  • Convert: \( \beta = 0.000378 \times 0.555556 \approx 0.00021 \, \text{1/°F} \)
  • \( \alpha = 1.17e-5 \times 0.555556 \approx 6.5e-6 \, \text{1/°F} \)
  • \( \Delta t = 2.78 \times 1.8 \approx 5 \, \text{°F} \)
  • \( D = 0.2545 \times 39.3701 \approx 10.02 \, \text{in.} \)
  • \( E = 2e11 \times 0.000145038 \approx 29007600 \, \text{psi} \)
  • \( \gamma = 4.5e-10 \times 6.89476e3 \approx 3.10264e-6 \, \text{in²/lb} \)
  • \( \Delta r = 0.009271 \times 39.3701 \approx 0.365 \, \text{in.} \)
  • Numerator: \( (0.00021 - 3 \times 6.5e-6) \times 5 \approx 0.0009525 \)
  • Denominator: \( 1.25 \times \frac{10.02}{29007600 \times 0.365} + 3.10264e-6 \approx 1.25 \times 9.465e-7 + 3.10264e-6 \approx 4.284e-6 \)
  • \( \Delta P = \frac{0.0009525}{4.284e-6} \approx 222.26 \, \text{psi} \)
  • Convert to Pa: \( 222.26 \times 6894.76 \approx 1532669 \)
  • Since 1532669 > 10000, display in scientific notation: \( 1.53267 \times 10^6 \)
• Example 3: For \( \beta = 0.0002 \, \text{1/°F} \), \( \alpha = 7e-6 \, \text{1/°F} \), \( \Delta t = 10 \, \text{°F} \), \( D = 4 \, \text{in.} \), \( E = 30000000 \, \text{psi} \), \( \gamma = 3e-6 \, \text{in²/lb} \), \( \Delta r = 0.237 \, \text{in.} \), pressure increase in psi:
  • Numerator: \( (0.0002 - 3 \times 7e-6) \times 10 = (0.0002 - 0.000021) \times 10 = 0.000179 \times 10 = 0.00179 \)
  • Denominator: \( 1.25 \times \frac{4}{30000000 \times 0.237} + 3e-6 \approx 1.25 \times \frac{4}{7110000} + 3e-6 \approx 1.25 \times 5.6259e-7 + 3e-6 \approx 7.0324e-7 + 3e-6 \approx 3.70324e-6 \)
  • \( \Delta P = \frac{0.00179}{3.70324e-6} \approx 483.22 \)
  • Since 483.22 < 10000 and > 0.00001, display with 5 decimal places: \( 483.22000 \)

5. Frequently Asked Questions (FAQ)

Q: What does pressure increase due to temperature change represent?
A: Pressure increase (\( \Delta P \)) quantifies the rise in pressure within a piping system due to thermal expansion of the fluid (e.g., water) and pipe material when the temperature increases, critical for system safety.

Q: How can I determine the input parameters?
A: Volumetric coefficient of thermal expansion (\( \beta \)) and compressibility (\( \gamma \)) are obtained from water property tables (e.g., \( \beta \approx 0.00021 \, \text{1/°F} \), \( \gamma \approx 3.1e-6 \, \text{in²/lb} \) at typical temperatures). Linear coefficient of thermal expansion (\( \alpha \)) and modulus of elasticity (\( E \)) depend on the pipe material (e.g., \( \alpha \approx 6.5e-6 \, \text{1/°F} \), \( E \approx 29e6 \, \text{psi} \) for steel). Temperature increase (\( \Delta t \)) is measured or designed. Pipe diameter (\( D \)) and wall thickness (\( \Delta r \)) are obtained from pipe specifications (e.g., Schedule 40).

Q: Why is pressure increase due to temperature change important in piping system design?
A: It ensures systems are designed to withstand pressure surges from temperature changes, preventing damage and ensuring safe, reliable operation.

Pressure Increase Due to Temperature Change Calculator© - All Rights Reserved 2025