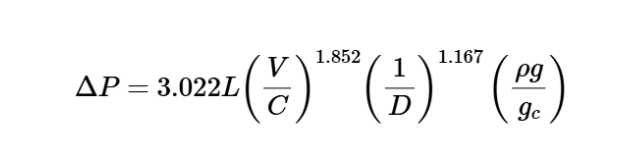Home Back

Pressure Drop (Hazen-Williams) Calculator

Pressure Drop (Hazen-Williams)

dimensionless

1. What is a Pressure Drop (Hazen-Williams) Calculator?

Definition: This calculator computes the pressure drop (\( \Delta P \)) in a pipe using the Hazen-Williams equation, commonly applied in sprinkler systems and water distribution networks.

Purpose: It is used in fluid dynamics and fire protection system design to quantify pressure losses due to friction, aiding in pipe sizing, pump selection, and system efficiency.

2. How Does the Calculator Work?

The calculator uses the following formula for pressure drop:

Pressure Drop: \[ \Delta P = 3.022 L \left( \frac{V}{C} \right)^{1.852} \left( \frac{1}{D} \right)^{1.167} \left( \frac{\rho g}{g_c} \right) \]

Where:

  • \( \Delta P \): Pressure drop (lb_f/ft², Pa)
  • \( L \): Length of pipe (ft, m)
  • \( V \): Average velocity (fps, m/s)
  • \( C \): Roughness factor (dimensionless)
  • \( D \): Internal diameter of pipe (ft, m)
  • \( \rho \): Fluid density (lb_m/ft³, kg/m³)
  • \( g \): Acceleration of gravity (ft/sec², m/s²)
  • \( g_c \): Units conversion factor (ft-lb_m/lb_f-sec², m-kg/N-s²)

Unit Conversions:

  • Length (\( L \)) and Diameter (\( D \)): ft, m (1 m = 3.28084 ft)
  • Velocity (\( V \)): fps, m/s (1 m/s = 3.28084 fps)
  • Fluid Density (\( \rho \)): lb_m/ft³, kg/m³ (1 kg/m³ = 0.062428 lb_m/ft³)
  • Acceleration of Gravity (\( g \)): ft/sec², m/s² (1 m/s² = 3.28084 ft/sec²)
  • Conversion Factor (\( g_c \)): ft-lb_m/lb_f-sec², m-kg/N-s² (1 m-kg/N-s² = 3.28084 ft-lb_m/lb_f-sec²)
  • Pressure Drop (\( \Delta P \)): lb_f/ft², Pa (1 lb_f/ft² = 47.8803 Pa)

Steps:

  • Enter the length of pipe (\( L \)), average velocity (\( V \)), roughness factor (\( C \)), internal diameter (\( D \)), fluid density (\( \rho \)), acceleration of gravity (\( g \)), and conversion factor (\( g_c \)), and select their units.
  • Convert \( L \), \( V \), \( D \), \( \rho \), \( g \), and \( g_c \) to ft, fps, ft, lb_m/ft³, ft/sec², and ft-lb_m/lb_f-sec², respectively.
  • Calculate the pressure drop using the formula.
  • Convert the result to the selected unit (lb_f/ft² or Pa).
  • Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Pressure Drop Calculation

Calculating pressure drop using the Hazen-Williams equation is crucial for:

  • Sprinkler System Design: Ensures adequate water pressure for fire protection systems.
  • Water Distribution Networks: Determines pressure losses to optimize pipe sizing and pump requirements.
  • Energy Efficiency: Minimizes energy consumption by reducing friction losses in fluid flow.

4. Using the Calculator

Examples:

  • Example 1: For \( L = 100 \, \text{ft} \), \( V = 4 \, \text{fps} \), \( C = 140 \), \( D = 0.1667 \, \text{ft} \), \( \rho = 62.4 \, \text{lb_m/ft³} \), \( g = 32.2 \, \text{ft/sec²} \), \( g_c = 32.2 \, \text{ft-lb_m/lb_f-sec²} \), pressure drop in lb_f/ft²:
    • \( \Delta P = 3.022 \times 100 \times \left( \frac{4}{140} \right)^{1.852} \times \left( \frac{1}{0.1667} \right)^{1.167} \times \left( \frac{62.4 \times 32.2}{32.2} \right) \approx 3.022 \times 100 \times 0.001134 \times 7.987 \times 62.4 \approx 8486 \)
    • Since 8486 < 10000, display with 5 decimal places: \( 8486.00000 \)
  • Example 2: For \( L = 30 \, \text{m} \), \( V = 1.2 \, \text{m/s} \), \( C = 130 \), \( D = 0.05 \, \text{m} \), \( \rho = 1000 \, \text{kg/m³} \), \( g = 9.81 \, \text{m/s²} \), \( g_c = 1 \, \text{m-kg/N-s²} \), pressure drop in Pa:
    • Convert: \( L = 30 \times 3.28084 \approx 98.4252 \, \text{ft} \)
    • \( V = 1.2 \times 3.28084 \approx 3.93701 \, \text{fps} \)
    • \( D = 0.05 \times 3.28084 \approx 0.164042 \, \text{ft} \)
    • \( \rho = 1000 \times 0.062428 \approx 62.428 \, \text{lb_m/ft³} \)
    • \( g = 9.81 \times 3.28084 \approx 32.1850 \, \text{ft/sec²} \)
    • \( g_c = 1 \times 3.28084 \approx 3.28084 \, \text{ft-lb_m/lb_f-sec²} \)
    • \( \Delta P = 3.022 \times 98.4252 \times \left( \frac{3.93701}{130} \right)^{1.852} \times \left( \frac{1}{0.164042} \right)^{1.167} \times \left( \frac{62.428 \times 32.1850}{3.28084} \right) \approx 297.342 \times 0.001372 \times 8.019 \times 612.282 \approx 20003.7 \, \text{lb_f/ft²} \)
    • Convert to Pa: \( 20003.7 \times 47.8803 \approx 957737 \)
    • Since 957737 > 10000, display in scientific notation: \( 9.57737 \times 10^5 \)
  • Example 3: For \( L = 50 \, \text{ft} \), \( V = 5 \, \text{fps} \), \( C = 150 \), \( D = 0.25 \, \text{ft} \), \( \rho = 60 \, \text{lb_m/ft³} \), \( g = 32.2 \, \text{ft/sec²} \), \( g_c = 32.2 \, \text{ft-lb_m/lb_f-sec²} \), pressure drop in lb_f/ft²:
    • \( \Delta P = 3.022 \times 50 \times \left( \frac{5}{150} \right)^{1.852} \times \left( \frac{1}{0.25} \right)^{1.167} \times \left( \frac{60 \times 32.2}{32.2} \right) \approx 151.1 \times 0.001937 \times 4.668 \times 60 \approx 81.97 \)
    • Since 81.97 < 10000 and > 0.00001, display with 5 decimal places: \( 81.97000 \)

5. Frequently Asked Questions (FAQ)

Q: What does pressure drop in the Hazen-Williams equation represent?
A: Pressure drop (\( \Delta P \)) quantifies the loss of pressure due to friction in a pipe, critical for ensuring adequate flow in sprinkler systems and water networks.

Q: How can I determine the input parameters?
A: Pipe length (\( L \)) and diameter (\( D \)) are measured. Average velocity (\( V \)) is calculated from flow rate and pipe area. Roughness factor (\( C \)) is obtained from tables based on pipe material (e.g., 140 for smooth pipes). Fluid density (\( \rho \)) is determined from fluid properties. Acceleration of gravity (\( g \)) is typically 32.2 ft/sec² or 9.81 m/s². The conversion factor (\( g_c \)) is 32.2 ft-lb_m/lb_f-sec² in US units or 1 m-kg/N-s² in SI units.

Q: Why is the Hazen-Williams equation important in pipe system design?
A: It provides a simplified method for calculating pressure losses in water-based systems, ensuring proper system performance and safety.

Pressure Drop (Hazen-Williams) Calculator© - All Rights Reserved 2025