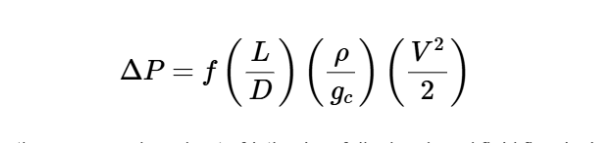Home Back

Pressure Drop Due to Friction Calculator

Pressure Drop Due to Friction

dimensionless

1. What is a Pressure Drop Due to Friction Calculator?

Definition: This calculator computes the pressure drop (\( \Delta P \)) due to friction in a fully developed fluid flow inside a pipe, using the Darcy-Weisbach equation.

Purpose: It is used in fluid dynamics and HVAC design to quantify pressure losses due to friction, aiding in pipe sizing, pump selection, and system efficiency.

2. How Does the Calculator Work?

The calculator uses the following formula for pressure drop:

Pressure Drop: \[ \Delta P = f \left( \frac{L}{D} \right) \left( \frac{\rho}{g_c} \right) \left( \frac{V^2}{2} \right) \]

Where:

  • \( \Delta P \): Pressure drop (lb_f/ft², Pa)
  • \( f \): Friction factor (dimensionless)
  • \( L \): Length of pipe (ft, m)
  • \( D \): Internal diameter of pipe (ft, m)
  • \( \rho \): Fluid density at mean temperature (lb_m/ft³, kg/m³)
  • \( V \): Average velocity (fps, m/s)
  • \( g_c \): Units conversion factor (ft-lb_m/lb_f-sec², m-kg/N-s²)

Unit Conversions:

  • Length (\( L \)) and Diameter (\( D \)): ft, m (1 m = 3.28084 ft)
  • Fluid Density (\( \rho \)): lb_m/ft³, kg/m³ (1 kg/m³ = 0.062428 lb_m/ft³)
  • Velocity (\( V \)): fps, m/s (1 m/s = 3.28084 fps)
  • Conversion Factor (\( g_c \)): ft-lb_m/lb_f-sec², m-kg/N-s² (1 m-kg/N-s² = 3.28084 ft-lb_m/lb_f-sec²)
  • Pressure Drop (\( \Delta P \)): lb_f/ft², Pa (1 lb_f/ft² = 47.8803 Pa)

Steps:

  • Enter the friction factor (\( f \)), length of pipe (\( L \)), internal diameter (\( D \)), fluid density (\( \rho \)), average velocity (\( V \)), and conversion factor (\( g_c \)), and select their units.
  • Convert \( L \), \( D \), \( \rho \), \( V \), and \( g_c \) to ft, ft, lb_m/ft³, fps, and ft-lb_m/lb_f-sec², respectively.
  • Calculate the pressure drop using the formula.
  • Convert the result to the selected unit (lb_f/ft² or Pa).
  • Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Pressure Drop Calculation

Calculating pressure drop due to friction is crucial for:

  • Pipe System Design: Determines pressure losses to ensure proper pipe sizing and pump requirements.
  • Energy Efficiency: Minimizes energy consumption by optimizing flow conditions and reducing friction losses.
  • System Performance: Ensures adequate fluid flow for industrial, HVAC, or plumbing applications.

4. Using the Calculator

Examples:

  • Example 1: For \( f = 0.02 \), \( L = 100 \, \text{ft} \), \( D = 0.1667 \, \text{ft} \), \( \rho = 62.4 \, \text{lb_m/ft³} \), \( V = 4 \, \text{fps} \), \( g_c = 32.2 \, \text{ft-lb_m/lb_f-sec²} \), pressure drop in lb_f/ft²:
    • \( \Delta P = 0.02 \times \left( \frac{100}{0.1667} \right) \times \left( \frac{62.4}{32.2} \right) \times \left( \frac{4^2}{2} \right) \approx 0.02 \times 599.88 \times 1.93789 \times 8 \approx 186.0 \)
    • Since 186.0 < 10000 and > 0.00001, display with 5 decimal places: \( 186.00000 \)
  • Example 2: For \( f = 0.025 \), \( L = 30 \, \text{m} \), \( D = 0.05 \, \text{m} \), \( \rho = 1000 \, \text{kg/m³} \), \( V = 1.2 \, \text{m/s} \), \( g_c = 1 \, \text{m-kg/N-s²} \), pressure drop in Pa:
    • Convert: \( L = 30 \times 3.28084 \approx 98.4252 \, \text{ft} \)
    • \( D = 0.05 \times 3.28084 \approx 0.164042 \, \text{ft} \)
    • \( \rho = 1000 \times 0.062428 \approx 62.428 \, \text{lb_m/ft³} \)
    • \( V = 1.2 \times 3.28084 \approx 3.93701 \, \text{fps} \)
    • \( g_c = 1 \times 3.28084 \approx 3.28084 \, \text{ft-lb_m/lb_f-sec²} \)
    • \( \Delta P = 0.025 \times \left( \frac{98.4252}{0.164042} \right) \times \left( \frac{62.428}{3.28084} \right) \times \left( \frac{3.93701^2}{2} \right) \approx 0.025 \times 599.88 \times 19.036 \times 7.749 \approx 2221.78 \, \text{lb_f/ft²} \)
    • Convert to Pa: \( 2221.78 \times 47.8803 \approx 106378.9 \)
    • Since 106378.9 > 10000, display in scientific notation: \( 1.06379 \times 10^5 \)
  • Example 3: For \( f = 0.018 \), \( L = 50 \, \text{ft} \), \( D = 0.25 \, \text{ft} \), \( \rho = 60 \, \text{lb_m/ft³} \), \( V = 5 \, \text{fps} \), \( g_c = 32.2 \, \text{ft-lb_m/lb_f-sec²} \), pressure drop in lb_f/ft²:
    • \( \Delta P = 0.018 \times \left( \frac{50}{0.25} \right) \times \left( \frac{60}{32.2} \right) \times \left( \frac{5^2}{2} \right) \approx 0.018 \times 200 \times 1.86335 \times 12.5 \approx 83.850 \)
    • Since 83.850 < 10000 and > 0.00001, display with 5 decimal places: \( 83.85000 \)

5. Frequently Asked Questions (FAQ)

Q: What does pressure drop due to friction represent?
A: Pressure drop (\( \Delta P \)) quantifies the loss of pressure in a pipe due to friction between the fluid and pipe walls, affecting flow efficiency.

Q: How can I determine the input parameters?
A: The friction factor (\( f \)) is obtained from Moody charts or equations based on pipe roughness and Reynolds number. Pipe length (\( L \)) and diameter (\( D \)) are measured. Fluid density (\( \rho \)) is determined from fluid properties at mean temperature. Average velocity (\( V \)) is calculated from flow rate and pipe area. The conversion factor (\( g_c \)) is typically 32.2 ft-lb_m/lb_f-sec² in US units or 1 m-kg/N-s² in SI units.

Q: Why is pressure drop important in pipe system design?
A: It ensures proper sizing of pipes and pumps to maintain desired flow rates, optimizing energy efficiency and system performance.

Pressure Drop Due to Friction Calculator© - All Rights Reserved 2025