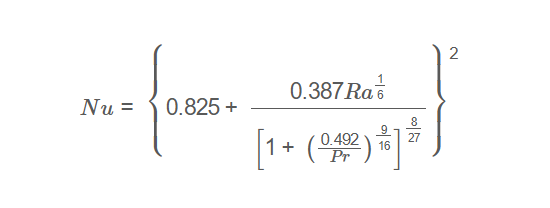1. What is a Natural Convection (Vertical Plate) Calculator?

Definition: This calculator computes the Prandtl number (\( Pr \)), Grashof number (\( Gr \)), Rayleigh number (\( Ra \)), and Nusselt number (\( Nu \)) for natural convection over a vertical plate, covering all Rayleigh number ranges.

Purpose: It is used in HVAC systems to determine heat transfer coefficients (\( h \)) for vertical surfaces, such as walls, enhancing passive cooling and heating design.

2. How Does the Calculator Work?

The calculator uses the following formulas for natural convection over a vertical plate:

Prandtl Number: \[ Pr = \frac{\mu}{\rho \alpha} \]

Grashof Number: \[ Gr = \frac{L^3 \rho^2 \beta g \Delta T}{\mu^2} \]

Rayleigh Number: \[ Ra = Gr Pr \]

Nusselt Number: \[ Nu = \left\{ 0.825 + \frac{0.387 Ra^{\frac{1}{6}}}{\left[ 1 + \left( \frac{0.492}{Pr} \right)^{\frac{9}{16}} \right]^{\frac{8}{27}}} \right\}^2 \]

Where:

• \( Nu \): Nusselt number (dimensionless)
• \( Pr \): Prandtl number (dimensionless)
• \( Gr \): Grashof number (dimensionless)
• \( Ra \): Rayleigh number (dimensionless)
• \( L \): Characteristic length (ft, in, m, e.g., height of the vertical plate)
• \( \rho \): Fluid density (lb/ft³, kg/m³)
• \( \beta \): Thermal expansion coefficient (1/°F, 1/°C)
• \( g \): Gravitational acceleration (32.174 ft/s²)
• \( \Delta T \): Temperature difference (\( |T_{\text{surface}} - T_{\text{fluid}}| \), °F, °C)
• \( \mu \): Dynamic viscosity (lb/ft-s, Pa-s)
• \( \alpha \): Thermal diffusivity (ft²/s, m²/s)

Unit Conversions:

• Characteristic Length (\( L \)): ft, in (1 in = \( \frac{1}{12} \) ft), m (1 m = 3.28084 ft)
• Fluid Density (\( \rho \)): lb/ft³, kg/m³ (1 kg/m³ = 0.062428 lb/ft³)
• Thermal Expansion Coefficient (\( \beta \)): 1/°F, 1/°C (1/°C = (9/5)/°F)
• Temperature Difference (\( \Delta T \)): °F, °C (1 °C = (9/5) °F)
• Dynamic Viscosity (\( \mu \)): lb/ft-s, Pa-s (1 Pa-s = 0.671969 lb/ft-s)
• Thermal Diffusivity (\( \alpha \)): ft²/s, m²/s (1 m²/s = 10.7639 ft²/s)

Steps:

• Enter the characteristic length (\( L \)), fluid density (\( \rho \)), thermal expansion coefficient (\( \beta \)), temperature difference (\( \Delta T \)), dynamic viscosity (\( \mu \)), and thermal diffusivity (\( \alpha \)), and select their units.
• Convert all inputs to base units (\( L \) to ft, \( \rho \) to lb/ft³, \( \beta \) to 1/°F, \( \Delta T \) to °F, \( \mu \) to lb/ft-s, \( \alpha \) to ft²/s).
• Calculate the Prandtl number using \( Pr = \frac{\mu}{\rho \alpha} \).
• Calculate the Grashof number using \( Gr = \frac{L^3 \rho^2 \beta g \Delta T}{\mu^2} \).
• Calculate the Rayleigh number using \( Ra = Gr Pr \).
• Calculate the Nusselt number using the given formula.
• Display \( Pr \), \( Gr \), \( Ra \), and \( Nu \), using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Natural Convection (Vertical Plate) Calculation

Calculating the Nusselt number for natural convection over a vertical plate is crucial for:

• HVAC Design: Determines heat transfer coefficients for vertical surfaces like walls, enhancing passive cooling and heating design.
• Energy Efficiency: Helps design systems that efficiently transfer heat via natural convection, reducing energy consumption.
• System Performance: Ensures accurate thermal load calculations for heating and cooling systems.

4. Using the Calculator

Examples:

• Example 1: For \( L = 1 \, \text{ft} \), \( \rho = 0.075 \, \text{lb/ft}^3 \), \( \beta = 0.0018 \, \text{1/°F} \), \( \Delta T = 20 \, \text{°F} \), \( \mu = 1.2 \times 10^{-5} \, \text{lb/ft-s} \), \( \alpha = 0.00015 \, \text{ft}^2\text{/s} \):
  • Prandtl Number: \( Pr = \frac{1.2 \times 10^{-5}}{0.075 \times 0.00015} \approx 1.0667 \)
  • Grashof Number: \( Gr = \frac{(1)^3 \times (0.075)^2 \times 0.0018 \times 32.174 \times 20}{(1.2 \times 10^{-5})^2} \approx 4.514 \times 10^7 \)
  • Rayleigh Number: \( Ra = 4.514 \times 10^7 \times 1.0667 \approx 4.815 \times 10^7 \)
  • Nusselt Number: \( \text{Term 1} = \left( \frac{0.492}{1.0667} \right)^{\frac{9}{16}}} \approx 0.6085 \), \( \text{Denominator} = \left( 1 + 0.6085 \right)^{\frac{8}{27}}} \approx 1.1590 \), \( \text{Term 2} = \frac{0.387 \times (4.815 \times 10^7)^{\frac{1}{6}}}}{1.1590} \approx 0.387 \times 10.2738 / 1.1590 \approx 3.4309 \), \( Nu = (0.825 + 3.4309)^2 \approx (4.2559)^2 \approx 18.1137 \)
• Example 2: For \( L = 0.5 \, \text{m} \), \( \rho = 1.2 \, \text{kg/m}^3 \), \( \beta = 0.0033 \, \text{1/°C} \), \( \Delta T = 15 \, \text{°C} \), \( \mu = 1.8 \times 10^{-5} \, \text{Pa-s} \), \( \alpha = 2.2 \times 10^{-5} \, \text{m}^2\text{/s} \):
  • Convert: \( L = 0.5 \times 3.28084 = 1.64042 \, \text{ft} \), \( \rho = 1.2 \times 0.062428 = 0.0749136 \, \text{lb/ft}^3 \), \( \beta = 0.0033 \times \frac{9}{5} = 0.00594 \, \text{1/°F} \), \( \Delta T = 15 \times \frac{9}{5} = 27 \, \text{°F} \), \( \mu = 1.8 \times 10^{-5} \times 0.671969 = 1.20954 \times 10^{-5} \, \text{lb/ft-s} \), \( \alpha = 2.2 \times 10^{-5} \times 10.7639 = 2.3681 \times 10^{-4} \, \text{ft}^2\text{/s} \)
  • Prandtl Number: \( Pr = \frac{1.20954 \times 10^{-5}}{0.0749136 \times 2.3681 \times 10^{-4}} \approx 0.6817 \)
  • Grashof Number: \( Gr = \frac{(1.64042)^3 \times (0.0749136)^2 \times 0.00594 \times 32.174 \times 27}{(1.20954 \times 10^{-5})^2} \approx 1.284 \times 10^8 \)
  • Rayleigh Number: \( Ra = 1.284 \times 10^8 \times 0.6817 \approx 8.753 \times 10^7 \)
  • Nusselt Number: \( \text{Term 1} = \left( \frac{0.492}{0.6817} \right)^{\frac{9}{16}}} \approx 0.7763 \), \( \text{Denominator} = \left( 1 + 0.7763 \right)^{\frac{8}{27}}} \approx 1.1998 \), \( \text{Term 2} = \frac{0.387 \times (8.753 \times 10^7)^{\frac{1}{6}}}}{1.1998} \approx 0.387 \times 11.7289 / 1.1998 \approx 3.7847 \), \( Nu = (0.825 + 3.7847)^2 \approx (4.6097)^2 \approx 21.2493 \)

5. Frequently Asked Questions (FAQ)

Q: What is the natural convection correlation for a vertical plate?
A: The correlation \( Nu = \left\{ 0.825 + \frac{0.387 Ra^{\frac{1}{6}}}{\left[ 1 + \left( \frac{0.492}{Pr} \right)^{\frac{9}{16}} \right]^{\frac{8}{27}}} \right\}^2 \) calculates the Nusselt number for natural convection over a vertical plate, covering all Rayleigh number ranges.

Q: Why is this calculation important in HVAC systems?
A: It determines heat transfer coefficients for vertical surfaces like walls, enhancing passive cooling and heating design in HVAC systems.

Q: How do I determine the characteristic length (\( L \))?
A: For a vertical plate, the characteristic length (\( L \)) is typically the height of the plate.

Natural Convection (Vertical Plate) Calculator© - All Rights Reserved 2025