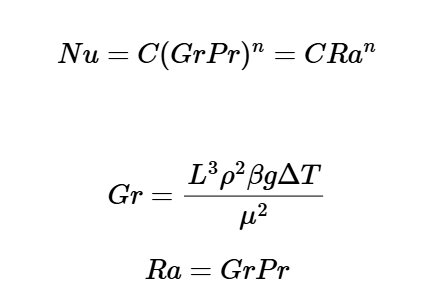1. What is a Natural Convection Correlation Calculator?

Definition: This calculator computes the Prandtl number (\( Pr \)), Grashof number (\( Gr \)), Rayleigh number (\( Ra \)), and Nusselt number (\( Nu \)) for natural convection, using the correlation \( Nu = C (Gr Pr)^n \).

Purpose: It is used in HVAC systems to determine heat transfer coefficients (\( h \)) for passive heat transfer scenarios, such as radiators.

2. How Does the Calculator Work?

The calculator uses the following formulas for natural convection:

Prandtl Number: \[ Pr = \frac{\mu}{\rho \alpha} \]

Grashof Number: \[ Gr = \frac{L^3 \rho^2 \beta g \Delta T}{\mu^2} \]

Rayleigh Number: \[ Ra = Gr Pr \]

Nusselt Number: \[ Nu = C Ra^n \]

Where:

• \( Nu \): Nusselt number (dimensionless)
• \( Pr \): Prandtl number (dimensionless)
• \( Gr \): Grashof number (dimensionless)
• \( Ra \): Rayleigh number (dimensionless)
• \( C, n \): Empirical constants (based on \( Ra \), e.g., \( C = 0.59 \), \( n = 0.25 \) for laminar, \( C = 0.10 \), \( n = 0.33 \) for turbulent)
• \( L \): Characteristic length (ft, in, m, e.g., height for vertical plates)
• \( \rho \): Fluid density (lb/ft³, kg/m³)
• \( \beta \): Thermal expansion coefficient (1/°F, 1/°C)
• \( g \): Gravitational acceleration (32.174 ft/s²)
• \( \Delta T \): Temperature difference (\( |T_{\text{surface}} - T_{\text{fluid}}| \), °F, °C)
• \( \mu \): Dynamic viscosity (lb/ft-s, Pa-s)
• \( \alpha \): Thermal diffusivity (ft²/s, m²/s)

Unit Conversions:

• Characteristic Length (\( L \)): ft, in (1 in = \( \frac{1}{12} \) ft), m (1 m = 3.28084 ft)
• Fluid Density (\( \rho \)): lb/ft³, kg/m³ (1 kg/m³ = 0.062428 lb/ft³)
• Thermal Expansion Coefficient (\( \beta \)): 1/°F, 1/°C (1/°C = (9/5)/°F)
• Temperature Difference (\( \Delta T \)): °F, °C (1 °C = (9/5) °F)
• Dynamic Viscosity (\( \mu \)): lb/ft-s, Pa-s (1 Pa-s = 0.671969 lb/ft-s)
• Thermal Diffusivity (\( \alpha \)): ft²/s, m²/s (1 m²/s = 10.7639 ft²/s)

Steps:

• Enter the characteristic length (\( L \)), fluid density (\( \rho \)), thermal expansion coefficient (\( \beta \)), temperature difference (\( \Delta T \)), dynamic viscosity (\( \mu \)), and thermal diffusivity (\( \alpha \)), and select their units.
• Convert all inputs to base units (\( L \) to ft, \( \rho \) to lb/ft³, \( \beta \) to 1/°F, \( \Delta T \) to °F, \( \mu \) to lb/ft-s, \( \alpha \) to ft²/s).
• Calculate the Prandtl number using \( Pr = \frac{\mu}{\rho \alpha} \).
• Calculate the Grashof number using \( Gr = \frac{L^3 \rho^2 \beta g \Delta T}{\mu^2} \).
• Calculate the Rayleigh number using \( Ra = Gr Pr \).
• Determine \( C \) and \( n \) based on \( Ra \):
  • If \( 10^4 < Ra < 10^9 \): \( C = 0.59 \), \( n = 0.25 \) (laminar)
  • If \( 10^9 \leq Ra < 10^{13} \): \( C = 0.10 \), \( n = 0.33 \) (turbulent)
• Calculate the Nusselt number using \( Nu = C Ra^n \).
• Display \( Pr \), \( Gr \), \( Ra \), and \( Nu \), using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Natural Convection Correlation Calculation

Calculating the Nusselt number for natural convection is crucial for:

• HVAC Design: Determines heat transfer coefficients for passive heat transfer in radiators and other components, optimizing system performance.
• Energy Efficiency: Helps design systems that efficiently transfer heat via natural convection, reducing energy consumption.
• System Performance: Ensures accurate thermal load calculations for heating and cooling systems.

4. Using the Calculator

Examples:

• Example 1: For \( L = 1 \, \text{ft} \), \( \rho = 0.075 \, \text{lb/ft}^3 \), \( \beta = 0.0018 \, \text{1/°F} \), \( \Delta T = 20 \, \text{°F} \), \( \mu = 1.2 \times 10^{-5} \, \text{lb/ft-s} \), \( \alpha = 0.00015 \, \text{ft}^2\text{/s} \):
  • Prandtl Number: \( Pr = \frac{1.2 \times 10^{-5}}{0.075 \times 0.00015} \approx 1.0667 \)
  • Grashof Number: \( Gr = \frac{(1)^3 \times (0.075)^2 \times 0.0018 \times 32.174 \times 20}{(1.2 \times 10^{-5})^2} \approx 4.514 \times 10^7 \)
  • Rayleigh Number: \( Ra = 4.514 \times 10^7 \times 1.0667 \approx 4.815 \times 10^7 \)
  • Flow Regime: Laminar (\( 10^4 < Ra < 10^9 \)), so \( C = 0.59 \), \( n = 0.25 \)
  • Nusselt Number: \( Nu = 0.59 \times (4.815 \times 10^7)^{0.25} \approx 0.59 \times 26.9215 \approx 15.8837 \)
• Example 2: For \( L = 0.5 \, \text{m} \), \( \rho = 1.2 \, \text{kg/m}^3 \), \( \beta = 0.0033 \, \text{1/°C} \), \( \Delta T = 15 \, \text{°C} \), \( \mu = 1.8 \times 10^{-5} \, \text{Pa-s} \), \( \alpha = 2.2 \times 10^{-5} \, \text{m}^2\text{/s} \):
  • Convert: \( L = 0.5 \times 3.28084 = 1.64042 \, \text{ft} \), \( \rho = 1.2 \times 0.062428 = 0.0749136 \, \text{lb/ft}^3 \), \( \beta = 0.0033 \times \frac{9}{5} = 0.00594 \, \text{1/°F} \), \( \Delta T = 15 \times \frac{9}{5} = 27 \, \text{°F} \), \( \mu = 1.8 \times 10^{-5} \times 0.671969 = 1.20954 \times 10^{-5} \, \text{lb/ft-s} \), \( \alpha = 2.2 \times 10^{-5} \times 10.7639 = 2.3681 \times 10^{-4} \, \text{ft}^2\text{/s} \)
  • Prandtl Number: \( Pr = \frac{1.20954 \times 10^{-5}}{0.0749136 \times 2.3681 \times 10^{-4}} \approx 0.6817 \)
  • Grashof Number: \( Gr = \frac{(1.64042)^3 \times (0.0749136)^2 \times 0.00594 \times 32.174 \times 27}{(1.20954 \times 10^{-5})^2} \approx 1.284 \times 10^8 \)
  • Rayleigh Number: \( Ra = 1.284 \times 10^8 \times 0.6817 \approx 8.753 \times 10^7 \)
  • Flow Regime: Laminar (\( 10^4 < Ra < 10^9 \)), so \( C = 0.59 \), \( n = 0.25 \)
  • Nusselt Number: \( Nu = 0.59 \times (8.753 \times 10^7)^{0.25} \approx 0.59 \times 30.8587 \approx 18.2066 \)

5. Frequently Asked Questions (FAQ)

Q: What is the natural convection correlation?
A: The natural convection correlation \( Nu = C (Gr Pr)^n \) relates the Nusselt number to the Rayleigh number (product of Grashof and Prandtl numbers), used to calculate the convective heat transfer coefficient (\( h \)) in natural convection scenarios.

Q: Why is natural convection important in HVAC systems?
A: It determines heat transfer rates in passive systems like radiators, ensuring efficient heating performance in HVAC systems.

Q: Where can I find the empirical constants (\( C \), \( n \))?
A: These constants depend on geometry and flow regime and are typically provided in engineering tables (e.g., Table 1-2 in the referenced pages). Common values for a vertical plate are \( C = 0.59 \), \( n = 0.25 \) for laminar flow (\( 10^4 < Ra < 10^9 \)), and \( C = 0.10 \), \( n = 0.33 \) for turbulent flow (\( 10^9 \leq Ra < 10^{13} \)).

Natural Convection Correlation Calculator© - All Rights Reserved 2025