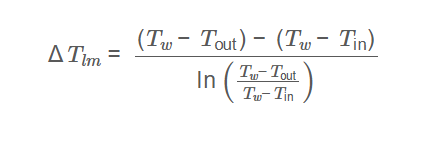1. What is a Log-Mean Temperature Difference Calculator?
Definition: This calculator computes the log-mean temperature difference (\( \Delta T_{lm} \)) for heat transfer in a pipe with constant wall temperature, used in fluid heating or cooling.
Purpose: It is used in HVAC systems to calculate the effective temperature difference driving heat transfer, optimizing fluid temperature control in piping systems.
2. How Does the Calculator Work?
The calculator uses the following formula for log-mean temperature difference:
Log-Mean Temperature Difference:
\[
\Delta T_{lm} = \frac{(T_w - T_{\text{out}}) - (T_w - T_{\text{in}})}{\ln \left( \frac{T_w - T_{\text{out}}}{T_w - T_{\text{in}}} \right)}
\]
Where:
- \( \Delta T_{lm} \): Log-mean temperature difference (°F, convertible to °C or K)
- \( T_w \): Wall temperature (°F, °C, K)
- \( T_{\text{in}} \): Inlet fluid temperature (°F, °C, K)
- \( T_{\text{out}} \): Outlet fluid temperature (°F, °C, K)
Unit Conversions:
- Temperatures (\( T_w \), \( T_{\text{in}} \), \( T_{\text{out}} \)): °F, °C (°F = °C × 9/5 + 32), K (°F = (K - 273.15) × 9/5 + 32)
- Log-Mean Temperature Difference (\( \Delta T_{lm} \)): °F, °C (°C = °F × 5/9), K (same as °C for differences)
Steps:
- Enter the wall temperature (\( T_w \)), inlet fluid temperature (\( T_{\text{in}} \)), and outlet fluid temperature (\( T_{\text{out}} \)), and select their units.
- Convert all temperatures to °F.
- Validate that the temperature differences \( T_w - T_{\text{out}} \) and \( T_w - T_{\text{in}} \) are not zero, and the ratio \( (T_w - T_{\text{out}}) / (T_w - T_{\text{in}}) \) is positive.
- Calculate the log-mean temperature difference using the formula.
- Convert the result to the selected unit (°F, °C, or K).
- Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Log-Mean Temperature Difference Calculation
Calculating the log-mean temperature difference is crucial for:
- HVAC Design: Determines the effective temperature difference for heat transfer in piping systems, aiding in the design of fluid heating or cooling.
- Energy Efficiency: Helps optimize pipe dimensions and flow rates to achieve desired temperature changes, reducing energy consumption.
- System Performance: Ensures accurate thermal load calculations for HVAC systems.
4. Using the Calculator
Examples:
- Example 1: For \( T_w = 150 \, \text{°F} \), \( T_{\text{in}} = 70 \, \text{°F} \), \( T_{\text{out}} = 110 \, \text{°F} \), LMTD in °F:
- \( T_w - T_{\text{out}} = 150 - 110 = 40 \)
- \( T_w - T_{\text{in}} = 150 - 70 = 80 \)
- Numerator: \( 40 - 80 = -40 \)
- Denominator: \( \ln \left( \frac{40}{80} \right) = \ln(0.5) \approx -0.6931 \)
- LMTD: \( \frac{-40}{-0.6931} \approx 57.7237 \, \text{°F} \)
- Example 2: For \( T_w = 80 \, \text{°C} \), \( T_{\text{in}} = 20 \, \text{°C} \), \( T_{\text{out}} = 50 \, \text{°C} \), LMTD in °C:
- Convert to °F: \( T_w = (80 \times 9/5) + 32 = 176 \, \text{°F} \), \( T_{\text{in}} = (20 \times 9/5) + 32 = 68 \, \text{°F} \), \( T_{\text{out}} = (50 \times 9/5) + 32 = 122 \, \text{°F} \)
- \( T_w - T_{\text{out}} = 176 - 122 = 54 \)
- \( T_w - T_{\text{in}} = 176 - 68 = 108 \)
- Numerator: \( 54 - 108 = -54 \)
- Denominator: \( \ln \left( \frac{54}{108} \right) = \ln(0.5) \approx -0.6931 \)
- LMTD: \( \frac{-54}{-0.6931} \approx 77.9137 \, \text{°F} \)
- Convert to °C: \( 77.9137 \times 5/9 \approx 43.2854 \, \text{°C} \)
5. Frequently Asked Questions (FAQ)
Q: What is the log-mean temperature difference?
A: The log-mean temperature difference (\( \Delta T_{lm} \)) is a measure of the effective temperature difference driving heat transfer in a system with varying temperature differences, such as in a pipe with constant wall temperature.
Q: Why is LMTD important in HVAC systems?
A: It is critical for designing heat exchangers and piping systems, ensuring accurate calculations of heat transfer rates for fluid heating or cooling.
Q: What if the temperature differences are zero or the logarithm is undefined?
A: The calculator checks for these conditions and displays an error if the temperature differences \( T_w - T_{\text{out}} \) or \( T_w - T_{\text{in}} \) are zero, or if the ratio \( (T_w - T_{\text{out}}) / (T_w - T_{\text{in}}) \) is not positive.
Log-Mean Temperature Difference Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back