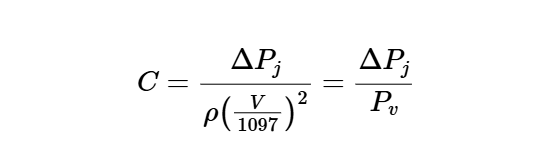Local Loss Coefficient for Fittings Calculator

Total Pressure Loss (\( \Delta P_j \)):

Air Density (\( \rho \)):

Velocity (\( V \)):

1. What is a Local Loss Coefficient Calculator?

Definition: This calculator computes the dimensionless local loss coefficient (\( C \)) for fittings, representing the ratio of total pressure loss to velocity pressure in HVAC ducts.

Purpose: It is used in HVAC design to quantify pressure losses caused by fittings (e.g., elbows, tees), aiding in fan selection and duct system efficiency.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Velocity Pressure: \[ P_v = \rho \left( \frac{V}{4005} \right)^2 \] Local Loss Coefficient: \[ C = \frac{\Delta P_j}{P_v} \]

Where:

\( C \): Local loss coefficient (dimensionless)
\( \Delta P_j \): Total pressure loss (in. of water, Pa)
\( P_v \): Velocity pressure (in. of water)
\( \rho \): Air density (lb_f/ft³, kg/m³)
\( V \): Velocity at referenced cross section (fpm, m/s)

Unit Conversions:

Total Pressure Loss (\( \Delta P_j \)): in. of water, Pa (1 Pa = 0.00401463 in. of water)
Air Density (\( \rho \)): lb_f/ft³, kg/m³ (1 kg/m³ = 0.062428 lb_f/ft³)
Velocity (\( V \)): fpm, m/s (1 m/s = 196.850 fpm)

Steps:

Enter the total pressure loss (\( \Delta P_j \)), air density (\( \rho \)), and velocity (\( V \)), and select their units.
Convert \( \Delta P_j \) to in. of water, \( \rho \) to lb_f/ft³, and \( V \) to fpm.
Calculate the velocity pressure (\( P_v \)).
Calculate the local loss coefficient (\( C \)).
Display the results with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Local Loss Coefficient Calculation

Calculating the local loss coefficient is crucial for:

HVAC System Design: Quantifies pressure losses due to fittings, ensuring accurate fan sizing and duct design.
Energy Efficiency: Minimizes energy consumption by optimizing duct layouts to reduce fitting losses.
System Performance: Ensures proper air distribution for effective ventilation and thermal comfort.

4. Using the Calculator

Examples:

Example 1: For \( \Delta P_j = 0.08 \, \text{in. of water} \), \( \rho = 0.075 \, \text{lb_f/ft³} \), \( V = 2000 \, \text{fpm} \), local loss coefficient:
- \( P_v = 0.075 \times \left( \frac{2000}{4005} \right)^2 \approx 0.075 \times 0.249219 \approx 0.018691 \, \text{in. of water} \)
- \( C = \frac{0.08}{0.018691} \approx 4.280 \)
- Since 0.018691 and 4.280 are < 10000 and > 0.00001, display with 5 decimal places: \( P_v = 0.01869 \, \text{in. of water} \), \( C = 4.28000 \)
Example 2: For \( \Delta P_j = 20 \, \text{Pa} \), \( \rho = 1.2 \, \text{kg/m³} \), \( V = 10 \, \text{m/s} \), local loss coefficient:
- Convert: \( \Delta P_j = 20 \times 0.00401463 \approx 0.080293 \, \text{in. of water} \)
- \( \rho = 1.2 \times 0.062428 \approx 0.074914 \, \text{lb_f/ft³} \)
- \( V = 10 \times 196.850 \approx 1968.50 \, \text{fpm} \)
- \( P_v = 0.074914 \times \left( \frac{1968.50}{4005} \right)^2 \approx 0.074914 \times 0.241462 \approx 0.018087 \, \text{in. of water} \)
- \( C = \frac{0.080293}{0.018087} \approx 4.438 \)
- Since 0.018087 and 4.438 are < 10000 and > 0.00001, display with 5 decimal places: \( P_v = 0.01809 \, \text{in. of water} \), \( C = 4.43800 \)
Example 3: For \( \Delta P_j = 0.1 \, \text{in. of water} \), \( \rho = 0.075 \, \text{lb_f/ft³} \), \( V = 3000 \, \text{fpm} \), local loss coefficient:
- \( P_v = 0.075 \times \left( \frac{3000}{4005} \right)^2 \approx 0.075 \times 0.560625 \approx 0.042047 \, \text{in. of water} \)
- \( C = \frac{0.1}{0.042047} \approx 2.378 \)
- Since 0.042047 and 2.378 are < 10000 and > 0.00001, display with 5 decimal places: \( P_v = 0.04205 \, \text{in. of water} \), \( C = 2.37800 \)

5. Frequently Asked Questions (FAQ)

Q: What does the local loss coefficient represent?
A: The local loss coefficient (\( C \)) quantifies the pressure loss caused by fittings in HVAC ducts, expressed as a ratio of total pressure loss to velocity pressure.

Q: How can I determine the total pressure loss, air density, and velocity?
A: Total pressure loss (\( \Delta P_j \)) is typically measured or obtained from fitting loss tables. Air density (\( \rho \)) can be calculated using the ideal gas law or standard tables (e.g., 0.075 lb_f/ft³ at 70°F). Velocity (\( V \)) is measured or calculated from air flow rate and duct area.

Q: Why is the local loss coefficient important in HVAC design?
A: It helps engineers account for pressure losses in fittings, ensuring accurate fan sizing and efficient duct system performance.