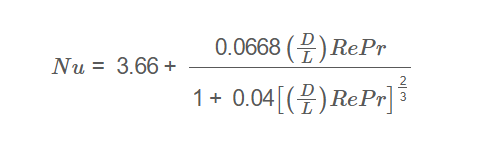Laminar Flow Entrance Length Correction Calculator for HVAC Systems

Laminar Flow Entrance Length Correction Calculator - Nusselt number

Pipe Diameter (\( D \)):

Pipe Length (\( L \)):

Reynolds Number (\( Re \)):

Prandtl Number (\( Pr \)):

1. What is a Laminar Flow Entrance Length Correction Calculator?

Definition: This calculator computes the Nusselt number (\( Nu \)) for laminar flow in circular pipes with thermal entrance effects, accounting for constant surface temperature.

Purpose: It is used in HVAC systems to calculate accurate heat transfer coefficients (\( h \)) in short pipes or ducts where entrance effects are significant.

2. How Does the Calculator Work?

The calculator uses the following formula for laminar flow entrance length correction:

Nusselt Number: \[ Nu = 3.66 + \frac{0.0668 \left( \frac{D}{L} \right) Re Pr}{1 + 0.04 \left[ \left( \frac{D}{L} \right) Re Pr \right]^{\frac{2}{3}}} \]

Where:

\( Nu \): Nusselt number (dimensionless)
\( D \): Pipe diameter (ft, in, m)
\( L \): Pipe length (ft, in, m)
\( Re \): Reynolds number (dimensionless, user input)
\( Pr \): Prandtl number (dimensionless, user input)

Unit Conversions:

Pipe Diameter (\( D \)) and Length (\( L \)): ft, in (1 in = \( \frac{1}{12} \) ft), m (1 m = 3.28084 ft)

Steps:

Enter the pipe diameter (\( D \)), pipe length (\( L \)), Reynolds number (\( Re \)), and Prandtl number (\( Pr \)), and select the units for \( D \) and \( L \).
Convert \( D \) and \( L \) to ft.
Validate that \( Re < 2300 \) (laminar flow requirement).
Calculate the Nusselt number using the given formula.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Laminar Flow Entrance Length Correction Calculation

Calculating the corrected Nusselt number for laminar flow entrance effects is crucial for:

HVAC Design: Provides accurate heat transfer coefficients (\( h \)) for short pipes or ducts, improving heat transfer predictions.
Energy Efficiency: Helps optimize heat exchanger design by accounting for entrance effects, reducing energy losses.
System Performance: Ensures accurate thermal load calculations in HVAC systems with short flow paths.

4. Using the Calculator

Examples:

Example 1: For \( D = 0.1 \, \text{ft} \), \( L = 2 \, \text{ft} \), \( Re = 2000 \), \( Pr = 0.7 \):
- \( \frac{D}{L} = \frac{0.1}{2} = 0.05 \)
- \( \left( \frac{D}{L} \right) Re Pr = 0.05 \times 2000 \times 0.7 = 70 \)
- Denominator: \( 1 + 0.04 \times (70)^{\frac{2}{3}}} \approx 1 + 0.04 \times 16.655 = 1.6662 \)
- Nusselt Number: \( Nu = 3.66 + \frac{0.0668 \times 70}{1.6662} \approx 3.66 + 2.8066 = 6.4666 \)
Example 2: For \( D = 0.05 \, \text{m} \), \( L = 1 \, \text{m} \), \( Re = 1500 \), \( Pr = 0.72 \):
- Convert: \( D = 0.05 \times 3.28084 = 0.164042 \, \text{ft} \), \( L = 1 \times 3.28084 = 3.28084 \, \text{ft} \)
- \( \frac{D}{L} = \frac{0.164042}{3.28084} = 0.05 \)
- \( \left( \frac{D}{L} \right) Re Pr = 0.05 \times 1500 \times 0.72 = 54 \)
- Denominator: \( 1 + 0.04 \times (54)^{\frac{2}{3}}} \approx 1 + 0.04 \times 14.279 = 1.5712 \)
- Nusselt Number: \( Nu = 3.66 + \frac{0.0668 \times 54}{1.5712} \approx 3.66 + 2.2966 = 5.9566 \)

5. Frequently Asked Questions (FAQ)

Q: What is the laminar flow entrance length correction?
A: It adjusts the Nusselt number for laminar flow in circular pipes to account for thermal entrance effects, particularly in short pipes with constant surface temperature.

Q: Why is this correction important in HVAC systems?
A: It ensures accurate heat transfer coefficient calculations in short HVAC ducts or pipes, improving heat exchanger design and system efficiency.

Q: How do I determine the Reynolds number (\( Re \)) and Prandtl number (\( Pr \))?
A: \( Re \) can be calculated using a Reynolds Number Calculator with fluid properties and geometry, while \( Pr \) depends on fluid properties like viscosity, specific heat, and thermal conductivity, often available in engineering references.