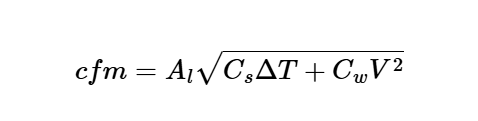1. What is an Infiltration Rate (Crack Method) Calculator?
Definition: This calculator computes the infiltration air flow rate (\( cfm \)) using the crack method, based on the effective leakage area, stack effect due to temperature difference, and wind effect.
Purpose: It is used in HVAC design to estimate the rate of outdoor air entering a building through cracks and leaks, aiding in the sizing of heating, cooling, and ventilation systems.
2. How Does the Calculator Work?
The calculator uses the following formula for infiltration rate:
Infiltration Rate:
\[
cfm = A_l \sqrt{C_s \Delta T + C_w V^2}
\]
Where:
- \( cfm \): Infiltration rate (ft³/min, m³/s)
- \( A_l \): Effective leakage area (in², cm²)
- \( C_s \): Stack coefficient (cfm²/in⁴-°F, m³/s²/cm⁴-K)
- \( \Delta T \): Indoor-outdoor temperature difference (°F, °C)
- \( C_w \): Wind coefficient (cfm²/in⁴-mph², m³/s²/cm⁴-(km/h)²)
- \( V \): Average wind speed (mph, km/h)
Unit Conversions:
- Leakage Area (\( A_l \)): in², cm² (1 cm² = 0.155000 in²)
- Stack Coefficient (\( C_s \)): cfm²/in⁴-°F, m³/s²/cm⁴-K (1 m³/s²/cm⁴-K ≈ 3.53147e7 cfm²/in⁴-°F)
- Temperature Difference (\( \Delta T \)): °F, °C (ΔT in °F = ΔT in °C × 9/5)
- Wind Coefficient (\( C_w \)): cfm²/in⁴-mph², m³/s²/cm⁴-(km/h)² (1 m³/s²/cm⁴-(km/h)² ≈ 2.58976e6 cfm²/in⁴-mph²)
- Wind Speed (\( V \)): mph, km/h (1 km/h = 0.621371 mph)
- Infiltration Rate (\( cfm \)): ft³/min, m³/s (1 ft³/min = 0.000471947 m³/s)
Steps:
- Enter the effective leakage area (\( A_l \)), stack coefficient (\( C_s \)), indoor-outdoor temperature difference (\( \Delta T \)), wind coefficient (\( C_w \)), and average wind speed (\( V \)), and select their units.
- Convert \( A_l \), \( C_s \), \( \Delta T \), \( C_w \), and \( V \) to in², cfm²/in⁴-°F, °F, cfm²/in⁴-mph², and mph, respectively.
- Calculate the infiltration rate using the formula.
- Convert the result to the selected unit (ft³/min or m³/s).
- Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.
3. Importance of Infiltration Rate Calculation
Calculating the infiltration rate is crucial for:
- HVAC Design: Determines the amount of outdoor air entering through cracks, affecting heating and cooling system sizing.
- Energy Efficiency: Identifies excessive infiltration, guiding improvements in building sealing to reduce energy losses.
- Indoor Air Quality: Ensures ventilation rates are balanced to maintain healthy indoor environments.
4. Using the Calculator
Examples:
- Example 1: For \( A_l = 1.968 \, \text{in²} \), \( C_s = 0.0299 \, \text{cfm²/in⁴-°F} \), \( \Delta T = 70 \, \text{°F} \), \( C_w = 0.0157 \, \text{cfm²/in⁴-mph²} \), \( V = 15 \, \text{mph} \), infiltration rate in ft³/min:
- \( C_s \Delta T = 0.0299 \times 70 = 2.093 \)
- \( C_w V^2 = 0.0157 \times 15^2 = 3.5325 \)
- \( cfm = 1.968 \sqrt{2.093 + 3.5325} \approx 1.968 \sqrt{5.6255} \approx 4.66666 \)
- Since 4.66666 < 10000 and > 0.00001, display with 5 decimal places: \( 4.66666 \)
- Example 2: For \( A_l = 12.7 \, \text{cm²} \), \( C_s = 8.467e-10 \, \text{m³/s²/cm⁴-K} \), \( \Delta T = 21 \, \text{°C} \), \( C_w = 6.067e-10 \, \text{m³/s²/cm⁴-(km/h)²} \), \( V = 24.14 \, \text{km/h} \), infiltration rate in m³/s:
- Convert: \( A_l = 12.7 \times 0.155000 = 1.9685 \, \text{in²} \)
- \( C_s = 8.467e-10 \times 3.53147e7 \approx 0.0299 \, \text{cfm²/in⁴-°F} \)
- \( \Delta T = 21 \times 9/5 = 37.8 \, \text{°F} \)
- \( C_w = 6.067e-10 \times 2.58976e6 \approx 0.0157 \, \text{cfm²/in⁴-mph²} \)
- \( V = 24.14 \times 0.621371 \approx 15 \, \text{mph} \)
- \( C_s \Delta T = 0.0299 \times 37.8 \approx 1.13022 \), \( C_w V^2 = 0.0157 \times 15^2 \approx 3.5325 \)
- \( cfm = 1.9685 \sqrt{1.13022 + 3.5325} \approx 1.9685 \sqrt{4.66272} \approx 4.25023 \, \text{ft³/min} \)
- Convert to m³/s: \( 4.25023 \times 0.000471947 \approx 0.0020058 \)
- Since 0.0020058 < 10000 and > 0.00001, display with 5 decimal places: \( 0.00201 \)
- Example 3: For \( A_l = 3 \, \text{in²} \), \( C_s = 0.02 \, \text{cfm²/in⁴-°F} \), \( \Delta T = 50 \, \text{°F} \), \( C_w = 0.01 \, \text{cfm²/in⁴-mph²} \), \( V = 10 \, \text{mph} \), infiltration rate in ft³/min:
- \( C_s \Delta T = 0.02 \times 50 = 1 \), \( C_w V^2 = 0.01 \times 10^2 = 1 \)
- \( cfm = 3 \sqrt{1 + 1} \approx 3 \sqrt{2} \approx 4.24264 \)
- Since 4.24264 < 10000 and > 0.00001, display with 5 decimal places: \( 4.24264 \)
5. Frequently Asked Questions (FAQ)
Q: What does the infiltration rate represent in the crack method?
A: The infiltration rate (\( cfm \)) quantifies the volume of outdoor air entering a building per minute through cracks, driven by stack effect (temperature difference) and wind pressure.
Q: How can I determine the effective leakage area and coefficients?
A: Effective leakage area (\( A_l \)) and coefficients (\( C_s \), \( C_w \)) are typically obtained from standards like ASHRAE (e.g., Tables 5-14, 5-15, 5-16), building tests, or manufacturer data.
Q: Why is the crack method used in HVAC design?
A: It provides a detailed estimate of infiltration through specific leakage paths, improving accuracy in heating and cooling load calculations compared to simpler methods.
Infiltration Rate (Crack Method) Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back