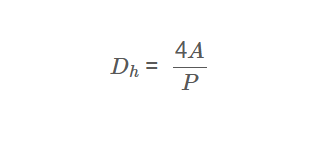Hydraulic Diameter Calculator for HVAC Systems

1. What is a Hydraulic Diameter Calculator?

Definition: This calculator computes the hydraulic diameter (\( D_h \)) for non-circular ducts or pipes using the formula, which relies on the cross-sectional area and wetted perimeter.

Purpose: It is used in fluid dynamics and HVAC systems to determine a characteristic length for non-circular ducts, essential for calculating flow regimes, Reynolds number, friction factor, and pressure drops.

2. How Does the Calculator Work?

The calculator uses the hydraulic diameter formula:

Hydraulic Diameter: \[ D_h = \frac{4A}{P} \] Where:

\( D_h \): Hydraulic diameter (ft, in, m)
\( A \): Cross-sectional area (ft², in², m²)
\( P \): Wetted perimeter (ft, in, m)

Unit Conversions:

Cross-Sectional Area (\( A \)): ft², in² (1 in² = \( \frac{1}{144} \) ft²), m² (1 m² = 10.7639 ft²)
Wetted Perimeter (\( P \)) and Hydraulic Diameter (\( D_h \)): ft, in (1 in = \( \frac{1}{12} \) ft), m (1 m = 3.28084 ft)

Steps:

Enter the cross-sectional area and wetted perimeter, and select their units.
Convert all inputs to base units (ft² for area, ft for perimeter).
Calculate the hydraulic diameter using \( D_h = \frac{4A}{P} \).
Convert the result to the selected unit (ft, in, m).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Hydraulic Diameter Calculation

Calculating the hydraulic diameter is crucial for:

HVAC Systems: Ensures accurate pressure drop calculations in non-circular ducts for efficient system design.
Fluid Dynamics: Enables the determination of flow regimes (laminar or turbulent) via the Reynolds number.
Engineering Applications: Assists in calculating friction losses and optimizing duct or pipe design in various industries.

4. Using the Calculator

Examples:

Example 1: For \( A = 2 \, \text{ft}^2 \), \( P = 8 \, \text{ft} \), hydraulic diameter in ft:
- Hydraulic Diameter: \( D_h = \frac{4 \times 2}{8} = 1.0000 \, \text{ft} \)
Example 2: For \( A = 144 \, \text{in}^2 \), \( P = 48 \, \text{in} \), hydraulic diameter in m:
- Convert: \( A = 144 \div 144 = 1 \, \text{ft}^2 \), \( P = 48 \div 12 = 4 \, \text{ft} \)
- Hydraulic Diameter: \( D_h = \frac{4 \times 1}{4} = 1.0000 \, \text{ft} \)
- Convert to m: \( D_h = 1.0000 \times 0.3048 = 0.3048 \, \text{m} \)

5. Frequently Asked Questions (FAQ)

Q: What is the hydraulic diameter?
A: The hydraulic diameter is a characteristic length used for non-circular ducts or pipes in fluid flow calculations, defined as \( D_h = \frac{4A}{P} \).

Q: Why is the hydraulic diameter important in HVAC systems?
A: It allows for accurate calculation of pressure drops and flow characteristics in non-circular ducts, which is critical for efficient HVAC system design.

Q: How do I determine the cross-sectional area and wetted perimeter?
A: For a rectangular duct, the cross-sectional area is width × height, and the wetted perimeter is the sum of all sides in contact with the fluid (2 × width + 2 × height).