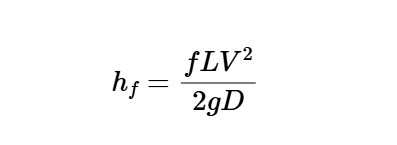Head Loss Due to Friction (Darcy-Weisbach for Steam) Calculator

Friction Factor (\( f \)): dimensionless

Length of Pipe (\( L \)):

Average Velocity (\( V \)):

Internal Diameter (\( D \)):

Acceleration of Gravity (\( g \)):

1. What is a Head Loss Due to Friction (Darcy-Weisbach for Steam) Calculator?

Definition: This calculator computes the head loss (\( h_f \)) due to friction in a pipe for steam flow, using the Darcy-Weisbach equation adapted for steam, expressed as the equivalent height of fluid column.

Purpose: It is used in steam system design to quantify energy losses due to friction, aiding in pipe sizing, pump selection, and system efficiency for steam flow applications.

2. How Does the Calculator Work?

The calculator uses the following formula for head loss:

Head Loss: \[ h_f = \frac{f L V^2}{2 g D} \]

Where:

\( h_f \): Head loss in feet of fluid flowing (ft, m)
\( f \): Friction factor (dimensionless)
\( L \): Length of pipe (ft, m)
\( V \): Average velocity (fps, m/s)
\( g \): Acceleration of gravity (ft/sec², m/s²)
\( D \): Internal diameter of pipe (ft, m)

Unit Conversions:

Length (\( L \)) and Diameter (\( D \)): ft, m (1 m = 3.28084 ft)
Velocity (\( V \)): fps, m/s (1 m/s = 3.28084 fps)
Acceleration of Gravity (\( g \)): ft/sec², m/s² (1 m/s² = 3.28084 ft/sec²)
Head Loss (\( h_f \)): ft, m (1 ft = 0.3048 m)

Steps:

Enter the friction factor (\( f \)), length of pipe (\( L \)), average velocity (\( V \)), internal diameter (\( D \)), and acceleration of gravity (\( g \)), and select their units.
Convert \( L \), \( V \), \( D \), and \( g \) to ft, fps, ft, and ft/sec², respectively.
Calculate the head loss using the formula.
Convert the result to the selected unit (ft or m).
Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.

3. Importance of Head Loss Calculation for Steam

Calculating head loss due to friction for steam flow is crucial for:

Steam System Design: Determines energy losses to ensure proper pipe sizing and system performance in steam applications.
Energy Efficiency: Minimizes energy consumption by optimizing flow conditions and reducing friction losses in steam distribution.
System Performance: Ensures adequate steam delivery for industrial processes, heating systems, or power generation.

4. Using the Calculator

Examples:

Example 1: For \( f = 0.0206 \), \( L = 37 \, \text{ft} \), \( V = 98.03 \, \text{fps} \), \( D = 0.2557 \, \text{ft} \), \( g = 32.2 \, \text{ft/sec²} \), head loss in ft:
- \( h_f = \frac{0.0206 \times 37 \times (98.03)^2}{2 \times 32.2 \times 0.2557} \approx \frac{0.0206 \times 37 \times 9609.8}{16.45828} \approx 446 \)
- Since 446 < 10000 and > 0.00001, display with 5 decimal places: \( 446.00000 \)
Example 2: For \( f = 0.025 \), \( L = 10 \, \text{m} \), \( V = 30 \, \text{m/s} \), \( D = 0.08 \, \text{m} \), \( g = 9.81 \, \text{m/s²} \), head loss in m:
- Convert: \( L = 10 \times 3.28084 \approx 32.8084 \, \text{ft} \)
- \( V = 30 \times 3.28084 \approx 98.4252 \, \text{fps} \)
- \( D = 0.08 \times 3.28084 \approx 0.262467 \, \text{ft} \)
- \( g = 9.81 \times 3.28084 \approx 32.1850 \, \text{ft/sec²} \)
- \( h_f = \frac{0.025 \times 32.8084 \times (98.4252)^2}{2 \times 32.1850 \times 0.262467} \approx \frac{0.025 \times 32.8084 \times 9687.52}{16.88467} \approx 471.24 \)
- Convert to m: \( 471.24 \times 0.3048 \approx 143.64 \)
- Since 143.64 < 10000 and > 0.00001, display with 5 decimal places: \( 143.64000 \)
Example 3: For \( f = 0.018 \), \( L = 50 \, \text{ft} \), \( V = 50 \, \text{fps} \), \( D = 0.5 \, \text{ft} \), \( g = 32.2 \, \text{ft/sec²} \), head loss in ft:
- \( h_f = \frac{0.018 \times 50 \times (50)^2}{2 \times 32.2 \times 0.5} \approx \frac{0.018 \times 50 \times 2500}{32.2} \approx 69.876 \)
- Since 69.876 < 10000 and > 0.00001, display with 5 decimal places: \( 69.87600 \)

5. Frequently Asked Questions (FAQ)

Q: What does head loss due to friction for steam represent?
A: Head loss (\( h_f \)) quantifies the energy loss due to friction in a pipe carrying steam, expressed as the equivalent height of fluid column, affecting system efficiency.

Q: How can I determine the input parameters?
A: The friction factor (\( f \)) is obtained from Moody charts or equations based on pipe roughness and Reynolds number for steam flow. Pipe length (\( L \)) and diameter (\( D \)) are measured. Average velocity (\( V \)) is calculated from steam flow rate and pipe area. Acceleration of gravity (\( g \)) is typically 32.2 ft/sec² in US units or 9.81 m/s² in SI units.

Q: Why is head loss important in steam system design?
A: It ensures proper sizing of pipes and equipment to maintain desired steam flow rates, optimizing energy efficiency and system performance for steam applications.