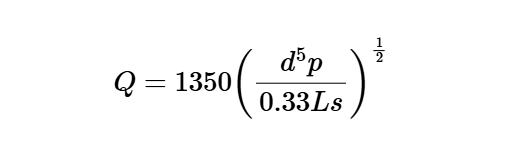1. What is a Gas Flow Rate (Pole Formula) Calculator?
Definition: This calculator computes the flow rate (\( Q \)) of gas in a low-pressure residential piping system, using the Pole formula, which accounts for pipe diameter, pressure drop, pipe length, and gas specific gravity.
Purpose: It is used in residential gas system design to determine the gas flow rate, aiding in pipe sizing, system efficiency, and ensuring adequate gas supply for appliances.
2. How Does the Calculator Work?
The calculator uses the following formula for gas flow rate:
Gas Flow Rate:
\[
Q = 1350 \left( \frac{d^5 p}{0.33 L s} \right)^{\frac{1}{2}}
\]
Where:
- \( Q \): Flow rate (ft³/hr, m³/s)
- \( d \): Nominal pipe diameter (in., m)
- \( p \): Pressure drop over length \( L \) (in. of water, Pa)
- \( L \): Length of pipe (ft, m)
- \( s \): Specific gravity of gas (dimensionless)
Unit Conversions:
- Pipe Diameter (\( d \)): in., m (1 m = 39.3701 in.)
- Pressure Drop (\( p \)): in. of water, Pa (1 Pa = 0.00401463 in. of water)
- Pipe Length (\( L \)): ft, m (1 m = 3.28084 ft)
- Flow Rate (\( Q \)): ft³/hr, m³/s (1 ft³/hr = 7.86579e-6 m³/s)
Steps:
- Enter the nominal pipe diameter (\( d \)), pressure drop (\( p \)), pipe length (\( L \)), and specific gravity (\( s \)), and select their units.
- Convert \( d \), \( p \), and \( L \) to in., in. of water, and ft, respectively.
- Calculate the flow rate using the formula.
- Convert the result to the selected unit (ft³/hr or m³/s).
- Display the result with 5 decimal places, or in scientific notation if the value is greater than 10,000 or less than 0.00001.
3. Importance of Gas Flow Rate Calculation
Calculating the gas flow rate using the Pole formula is crucial for:
- Residential Gas System Design: Ensures pipes are sized to deliver sufficient gas to appliances like heaters and stoves.
- Safety and Efficiency: Prevents pressure drops that could impair appliance performance or safety.
- System Optimization: Balances pipe size and cost while meeting gas demand.
4. Using the Calculator
Examples:
- Example 1: For \( d = 1 \, \text{in.} \), \( p = 0.3 \, \text{in. of water} \), \( L = 15 \, \text{ft} \), \( s = 0.60 \), flow rate in ft³/hr:
- \( Q = 1350 \left( \frac{1^5 \times 0.3}{0.33 \times 15 \times 0.60} \right)^{\frac{1}{2}} \approx 1350 \times \sqrt{\frac{0.3}{2.97}} \approx 1350 \times \sqrt{0.10101} \approx 1350 \times 0.31797 \approx 429.3 \)
- Since 429.3 < 10000 and > 0.00001, display with 5 decimal places: \( 429.30000 \)
- Example 2: For \( d = 0.0254 \, \text{m} \), \( p = 74.7 \, \text{Pa} \), \( L = 4.572 \, \text{m} \), \( s = 0.65 \), flow rate in m³/s:
- Convert: \( d = 0.0254 \times 39.3701 \approx 1 \, \text{in.} \)
- \( p = 74.7 \times 0.00401463 \approx 0.3 \, \text{in. of water} \)
- \( L = 4.572 \times 3.28084 \approx 15 \, \text{ft} \)
- \( Q = 1350 \left( \frac{1^5 \times 0.3}{0.33 \times 15 \times 0.65} \right)^{\frac{1}{2}} \approx 1350 \times \sqrt{\frac{0.3}{3.2175}} \approx 1350 \times \sqrt{0.09324} \approx 1350 \times 0.30535 \approx 412.22 \, \text{ft³/hr} \)
- Convert to m³/s: \( 412.22 \times 7.86579e-6 \approx 0.003243 \)
- Since 0.003243 < 10000 and > 0.00001, display with 5 decimal places: \( 0.00324 \)
- Example 3: For \( d = 0.75 \, \text{in.} \), \( p = 0.5 \, \text{in. of water} \), \( L = 20 \, \text{ft} \), \( s = 0.55 \), flow rate in ft³/hr:
- \( Q = 1350 \left( \frac{(0.75)^5 \times 0.5}{0.33 \times 20 \times 0.55} \right)^{\frac{1}{2}} \approx 1350 \times \sqrt{\frac{0.237304 \times 0.5}{3.63}} \approx 1350 \times \sqrt{0.03269} \approx 1350 \times 0.1808 \approx 244.08 \)
- Since 244.08 < 10000 and > 0.00001, display with 5 decimal places: \( 244.08000 \)
5. Frequently Asked Questions (FAQ)
Q: What does gas flow rate in the Pole formula represent?
A: Gas flow rate (\( Q \)) quantifies the volume of gas delivered per unit time in a low-pressure residential piping system, critical for meeting appliance demand.
Q: How can I determine the input parameters?
A: Nominal pipe diameter (\( d \)) is obtained from pipe specifications. Pressure drop (\( p \)) is measured or designed for the system (typically small, e.g., 0.3 in. of water). Pipe length (\( L \)) is measured along the pipe run. Specific gravity (\( s \)) is determined from gas properties (e.g., 0.60 for natural gas relative to air).
Q: Why is gas flow rate important in residential gas system design?
A: It ensures pipes are sized to deliver sufficient gas for safe and efficient appliance operation, optimizing system performance and cost.
Gas Flow Rate (Pole Formula) Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back